为什么使用交叉熵损失函数

为什么使用交叉熵损失函数而不是二次代价函数

本文基本转自这篇文章，感谢作者

前奏

1. 作为神经网络，应当具有自学习的能力，为了更好的模拟人学习的过程，神经网络的学习能力应当能够自我调整，当发现自己犯的错误越大时，改正的力度就越大。比如投篮：当运动员发现自己的投篮方向离正确方向越远，那么他调整的投篮角度就应该越大，篮球就更容易投进篮筐。这所谓的学习能力便体现在损失函数中，常见的损失函数有两种：二次代价函数和交叉熵损失函数，前者主要用在线性回归中，而在神经网络中主要用后者，下面我们来说明为什么。

2. 以一个神经元的二类分类训练为例，进行两次实验,激活函数采用$sigmoid$：输入一个相同的样本数据x=1.0（该样本对应的实际分类y=0）；两次实验各自随机初始化参数，从而在各自的第一次前向传播后得到不同的输出值，形成不同的$Loss$：

   

   

   在实验1中，随机初始化参数，使得第一次输出值为0.82（该样本对应的实际值为0）;经过300次迭代训练后，输出值由0.82降到0.09，逼近实际值。而在实验2中，第一次输出值为0.98，同样经过300迭代训练，输出值只降到了0.20。
   从两次实验的代价曲线中可以看出：实验1的代价随着训练次数增加而快速降低，但实验2的代价在一开始下降得非常缓慢；直观上看，初始的误差越大，收敛得越缓慢。

下面计算两种损失函数,eg:$y$是真实值,$\hat y$是计算值,$z=wx+b$,$\hat y = \sigma (z)$

二次代价损失函数

$$C=\frac{1}{2n}\sum_x|y-\hat y |^2$$

以一个样本为例:

$$L=\frac{(y-\hat y)^2}{2}$$

则有

$$\begin{align} \frac{\partial L}{\partial w} &=\frac{\partial L}{\partial \hat y} \frac{\partial \hat y}{\partial z} \frac{\partial z}{\partial w} \\ &=(\hat y-y) \sigma\prime(x)x \end{align}$$ $$\begin{align} \frac{\partial L}{\partial w} &=\frac{\partial L}{\partial \hat y} \frac{\partial \hat y}{\partial z} \\ &=(\hat y-y) \sigma\prime(x) \end{align}$$

其中，z表示神经元的输入，表示激活函数。从以上公式可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。而神经网络常用的激活函数为sigmoid函数，该函数的曲线如下所示:

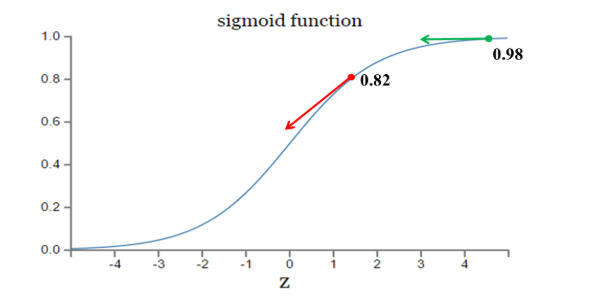
如图所示，实验2的初始输出值（0.98）对应的梯度明显小于实验1的输出值（0.82），因此实验2的参数梯度下降得比实验1慢。这就是初始的代价（误差）越大，导致训练越慢的原因。与我们的期望不符，即：不能像人一样，错误越大，改正的幅度越大，从而学习得越快。

交叉熵损失函数

$$C=\frac{1}{n}\sum_x[y\ln \hat y+(1-y)\ln (1-\hat y)]$$

以一个样本为例:

$$L=-\sum_x[y\ln \hat y+(1-y)\ln (1-\hat y)]$$

则有

$$\begin{align} \frac{\partial L}{\partial w}&=-\sum_x[\frac{y}{\hat y}-\frac{(1-y)}{1-\hat y}] \frac{\partial \hat y}{\partial z}\frac{\partial z}{\partial w}\\ &=-\sum_x[\frac{y}{\hat y}-\frac{(1-y)}{1-\hat y}]\sigma \prime(x)x\\ &=-\sum_x[\frac{y- \sigma (x)}{\sigma(x)(1-\sigma(x))}] \sigma \prime(x) x \\ &= -\sum_x[y-\hat y]x \end{align}$$ $$\begin{align} \frac{\partial L}{\partial b}&=-\sum_x[y-\hat y] \end{align}$$

因此，$w$的梯度公式中$\sigma \prime (z)$原来的被消掉了;另外，该梯度公式中的表示输出值与实际值之间的误差。所以，当误差越大，梯度就越大，参数$w$调整得越快，训练速度也就越快,$b$的梯度同理.

交叉熵函数来源

以$w$的偏导为例:在二次代价函数中:

$$\frac{\partial L}{\partial w} = (\hat y - y) \sigma \prime(x) x$$

为了消除$\sigma \prime(x)$,我们令要计算的$w$偏导为:

$$\frac{\partial L}{\partial w} = (\hat y - y) x$$

而$w$偏导实际计算为:

$$\begin{align} \frac{\partial L}{\partial w} &=\frac{\partial L}{\partial \hat y}\sigma \prime(x)x \\ &=\frac{\partial L}{\partial \hat y}\hat y(1-\hat y) x \\ \end{align}$$

则:

$$\frac{\partial L}{\partial \hat y}\hat y(1-\hat y) x= (\hat y - y) x$$

x被消掉得:

$$\frac{\partial L}{\partial \hat y} = \frac{\hat y-y}{(1-\hat y)\hat y}$$

求积分得:

$$L=-[y \ln \hat y +(1-y) \ln (1- \hat y)]$$

即交叉熵函数.