CNN的卷积层和普通神经网络全连接层对比

为了过渡，首先看一下这篇笔记

举例: 只有一个数据:$6\times6$,$Filter:3\times3$,如图所示:


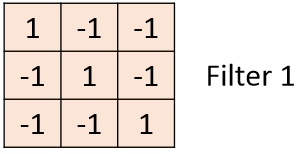
全连接神经网络

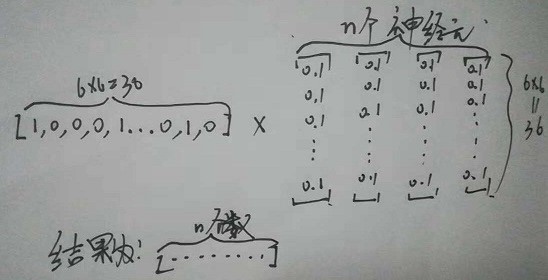
参数数量为 $(6\times 6+1)\times n$

CNN

参数数量为 $(3\times 3+1)\times n$

对比

可以很明显的看出，其实两者相差并不很多，其实feather map数量就是全连接层中的神经元数量，由于每个神经元所含参数只有9个，不能像全连接(每个神经元36个参数)那样按照矩阵相乘想乘得到一个数字，因此是用卷积的方式得到一个feather map，卷积过程中36个数据共享9个参数。

其他

  1. 很明显，通过卷积+池化+全连接层也能反向传播
  2. 其实能学到东西，关键在于初始化$Weights$，在普通全连接神经网络中: 
1
2
3
4
5
6
7
8
9
10
def add_layer(inputs, in_size, out_size, activation_function=None):
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
        output = tf.nn.dropout(output, keep_prob)
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs

在cnn的卷积层中: 

1
2
3
4
5
6
7
def conv2d(input, shape, activation_function):
    Weights = tf.Variable(tf.truncated_normal(shape=shape, stddev=0.1))
    biases = tf.constant(0.1, shape=[1, shape[3]])
    convOutput = tf.nn.conv2d(input, filter=Weights, strides=[1, 1, 1, 1], padding='SAME') + biases
    if activation_function:
        convOutput = activation_function(convOutput)
    return convOutput

也就是说，同一层中多个神经元的参数初始化是随机的，千万不能初始化为同一个值，这样会导致每个神经元的输出永远相同，也就是每个神经元学到的东西是相同的！！！每个神经元初始化Weights的不同是每个神经元学到不同特征的前提.