boosting

boosting 是一种特殊的集成学习方法。所有的‘基’分类器都是弱学习器，但通过采用特定的方式迭代，每次根据训练过的学习器的预测效果来更新样本权值,用于新的一轮学习,最终提高联合后的学习效果boosting。

AdaBoost

步骤:

1. 首先，是初始化训练数据的权值分布D1。假设有N个训练样本数据，则每一个训练样本最开始时，都被赋予相同的权值:w1=1/N。
2. 然后，训练弱分类器$G_i$.具体训练过程中是:如果某个训练样本点，被弱分类器$G_i$准确地分类,那么在构造下一个训练集中,它对应的权值要减小;相反,如果某个训练样本点被错误分类,那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
3. 最后，将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。
   换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。

流程

输入:训练数据集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$
输出:分类器G(x)

1. 每个训练样本初始化相同权值,即$w_i=1/N,得到$: $$D_1=(w_{11},w_{12},...,w_{1N}),w_{1i}=\frac{1}{N}$$
2. 开始迭代$m=1$~$M$
   a. 选取当前权值分布下误差率最低的分类器G为第m个基本分类器$G_m$,并计算误差: $$e_m=\sum_{t=1}^NP(G_m(x_i)≠y_i)=\sum_{i=1}^Nw_{mi}I(G_m(x_i)≠y_i)$$ b. 计算分类器权重: $$\alpha_m=\frac{1}{2}\ln \frac{1-e_m}{e_m}$$ 此处需要备注:当$e_m$<1 2时,$\alpha_m$>0,且$\alpha_m$随着$e_m$的增大而减少,即分类误差越小该弱分类器权值越大,意味着在最终的全国分类器中该弱分类器的权值大。

c. 更新样本权值分布$D_{t+1}$:

$$\begin{gather} D_{m+1}=(w_{m+1,1},w_{m+1,2},...,w_{m+1,N}) \\ w_{m+1,i}=\frac{w_{mi}}{Z_m} e^{-\alpha y_iG_m(x_i)} \end{gather}$$

其中,$Z_m$是规范化因子:

$$Z_m=\sum_i^N w_{mi}e^{-\alpha_m y_i G_m(x_i)}=2 \sqrt{e_m(1-e_m)}(可证)$$

此处需要备注:可以看出:

$$w_{m+1,i} = \begin{cases} \frac{w_{mi}}{Z_m}e^{-alpha_m} & G_m(x_i) = y_i( G_m(x_i) \times y_i =1) \\ \frac{w_{mi}}{Z_m}e^{alpha_m} & G_m(x_i) ≠ y_i(G_m(x_i) \times y_i = -1) \\ \end{cases}$$

意味着某样本分类错误时候该样本权值扩大,即所谓的更加关注该样本.

1. 组合分类器 $$f(x) = \sum_{m=1}^M \alpha_m G_m(x_i)$$ 得到最终分类器: $$G(x) = sign(f(x))=sign(\sum_{m=1}^M \alpha_m G_m(x_i))$$ $$\begin{align} f(x) &=sign(F(x)) \\ &=\sum_{k=1}^K \alpha_kT_k(x;\beta_k) \end{align}$$

   Boosting Tree(提升树算法)

   模型

   采用加法模型,利用前向分布算法,第m步得到的模型为: $$f_m(x)=f_{m-1}(x)+T(x;\Theta_m)$$ 其中$T(x;\Theta_m)$表示第m部要得到的决策树,$\Theta_m$表示其参数,并通过经验风险极小化来确定$\Theta_m$: $$\hat{\Theta}_m=\arg \min_{\Theta_m} \sum_{i=1}^NL(y_i,f_{m-1}(x_i)+T(x_i;\Theta_m))$$

   学习过程

   $$\begin{align} f_0(x)&=0 \\ f_m(x)&=f_{m-1}(x)+T(x;\Theta_m) \\ f_m(x)&=\sum_{m=1}^M T(x;\Theta_m) \end{align}$$ 当使用平方误差损失函数时: $$L(y,f(x))=(y-f(x))^2$$ 即: $$\begin{align} L(y,f_{m-1}(x)+T(x;\Theta_m))&=(y-f_{m-1}(x)-T(x;\Theta_m))^2 \\ &=(r-T(x;\Theta_m))^2 \end{align}$$ 其中$r=y-f_{m-1}(x)$,即第m-1论求得的树还剩下的残差,现在第m轮的目标是减少这个残差.

梯度提升

主要思想和上诉算法相同,不同点在于使用负梯度(伪残差)代替残差

1. 初始化 $$f_0(x) = \arg \min_c \sum_{i=1}^N L(y_i,c)$$

   也就是说$f_0(x)$其实是一个常数函数

2. 对m=1,2,3…,M
   a. 对i=1,2,3…,N,计算伪残差: $$r_{mi}=-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)}$$

b. 使用该残差列表$(x_i,r_{mi})$计算新的分类器$f_m(x)$(即基函数,可能是决策树、逻辑回归、SVM等)

c. 计算步长(也就是所谓的学习率,在Boosting中称为权重)

$$\gamma _m=\arg \min_{\gamma} \sum_{i=1}^N L(y_i,f_{m-1}-\gamma f_m(x))$$

计算步长可以用线性搜索的方式

d. 更新模型:

$$f_m(x) = f_{m-1}(x)+\gamma_m f(x)$$

GBDT

当上诉梯度提升使用的是基函数是CART的时候就是GBDT,且无论GBDT用来回归还是分类CART均用回归树

伪代码为: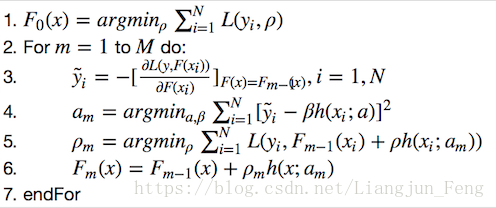

XGboost

补充:损失函数：计算的是一个样本的误差代价函数：是整个训练集上所有样本误差的平均目标函数：代价函数 + 正则化项

目标函数为:

$$Obj=\sum_{i=1}^n l(y_i,\hat{y_i})+\sum_t^K \Omega(f_t)$$

第一项是loss,第二项是正则项:

$$\Omega(f_t) = \gamma T + \frac{1}{2}\lambda\sum_{j=1}^T w_j^2$$

其中$w_j^2$是叶子节点j的权重.
由于新生成的树要拟合上次预测的损失,因此有:

$$\hat{y_i} = \hat{y_i}^{(t-1)} + f_t(x_i)$$

同时,可以将目标函数改写为:

$$Obj^t=\sum_{i=1}^n l(y_i,\hat{y_i}^{(t-1)}+f_t(x_i))+\Omega(f_t)$$

二阶泰勒展开:

$$Obj^t≈ \sum_{i=1}^n[l(y_i,\hat{y}^{(t-1)})+g_if_t(x_i)+\frac{1}{2} h_i f_t^2(x_i)]+\Omega(f_t)$$

其中$g_i$和$h_i$分别是一阶和二阶导数.可以直接去掉t-1棵树的残差:

$$g_i = \frac{\partial ^ \prime l(y_i,\hat{y}^{(t-1)})}{\partial \hat{y}^{(t-1)}} \\ h_i = \frac{\partial ^2 l(y_i,\hat{y}^{(t-1)})}{\partial \hat{y}^{(t-1)}} \\ Obj^t≈ \sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}f_t^2(x_i))]+\Omega(f_t)$$

将目标函数按照叶子节点展开:

$$\begin{align} Obj^t &≈ \sum_{i=1}^n[l(y_i,\hat{y}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}f_t^2(x_i)]+\Omega(f_t) \\ &=\sum_{i=1}^n[l(y_i,\hat{y}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}f_t^2(x_i)]+\gamma T + \frac{1}{2}\lambda\sum_{j=1}^T w_j^2 \\ &=\sum_{j=1}^T[(\sum_{i \in I_j} g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i + \lambda)w_j^2]+\gamma T \end{align}$$

最终目标函数为:

$$w_j^* = -\frac{G_j}{H_j+\lambda} \\ Obj^t = -\frac{1}{2}\sum_{j=1}^T \frac{G_j^2}{H_j+\lambda}+ \gamma T$$

其中:

$$G_j = \sum_{i \in I} g_i \\ H_j = \sum_{i \in I} h_i$$

$Obj^t$是每一步的目标函数,我们要让$Obj^t$小,就需要让$ \frac{G_j^2}{H_j+\lambda}$大,因此我们在这个地方更改决策树的split方案:
对于任意一个划分必能将数据划分为一个二叉树,则我们计算每一个可能的划分:

$$Gain=\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda} -\gamma$$

前两项是划分后左右两个子树的得分,第三项是不划分的得分,现在需要计算所有可能的划分,然后选择最大的划分左右子树。

XGboost和GBDT对比

1. 传统GBDT以CART作为基分类器，xgboost还支持线性分类器
2. 传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数
3. xgboost在代价函数里加入了正则项，用于控制模型的复杂度

前向分布算法

输入: 训练数据集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$,损失函数$L(y_i,f(x_i))$,基函数集${b(x;\lambda)}$

这里的基函数集应该指的是未知参数的某种分类器,而在前向分布算法中我们每一步都可以使用不同得分类器(虽然一般是相同得分类器),因此可以是基函数”集”.

输出: 加法模型$f(x)$
步骤:

1. 初始化$f_0(x)$
2. 对$m=1,2,…,M$
   a. $(\beta_M,\lambda_m)=arg\min_{\beta,\lambda}\sum_{i=1}^NL(y_i,f_{m-1}(x_i)+\beta b(x_i;\lambda))$
   b. 更新$f_m(x)=f_{m-1}(x)+\beta_m b(x;\lambda_m)$
3. 得到最终加法模型:$f(x)=f_M(x)=\sum_{m=1}^M \beta_mb(x;\lambda_m)$

从前向分布算法到Adaboost

简单来说,Adaboost就是当损失函数为指数损失函数时的前向分布算法,得到的是二分类模型

对于Adaboost最终分类器是:

$$f(x)=\sum_{m=1}^M \alpha_mG_m(x) \tag{5.1}$$

假设在Adaboost步骤第2步中,已经进行m-1轮迭代,得到:

$$\begin{align} f_{m-1}(x)&=f_{m-2}(x)+\alpha_{m-1}G_{m-1} \\ &=\alpha_1G_1(x)+...+\alpha_{m-1}G_{m-1}(x) \tag{5.2} \end{align}$$

在第m轮我们得到:

$$f_m(x)=f_{m-1}(x)+\alpha_mG_m(x) \tag{5.3}$$

目标是使前向分布算得到的$\alpha$和$G_m(x)$在训练数据集$T$上的损失函数最小,即:

$$(\alpha_m,G_m(x))=arg\min_{\alpha,G}\sum_{i=1}^Ne^{-y_i(f_{m-1}+\alpha G(x_i))} \tag{5.4}$$

令其为:

$$(\alpha_m,G_m(x))=arg\min_{\alpha,G}\sum_{i=1}^N \overline w_{mi} e^{-y_i\alpha G(x_i))} \tag{5.5}$$

其中$\overline w_{mi}=e^{-y_if_{m-1}}$,可以看出$\overline w_{mi}$与$\alpha$和$G(x)$无关,故与最小化无关,但是和$f_{m-1}$有关,故每一轮都有变化。
现在要证明的是使式5.5达到最小的$\alpha^*$和$G^*(x)$就是Adaboost算法所得到的$\alpha_m$和$G_m(x)$现在对两者分别求值:
首先,对于$G_m^*(x)$,对任意$\alpha$>0有:

$$G_m(x)^*=arg\min_G\sum_{i=1}^N\overline w_{mi}I(y_i≠G(x_i)) \tag{5.6}$$

该分类器$G_m^*(x)$就是式第m轮分类误差最小的分类器.然后求$\alpha^*_m$,参照式5.4和5.5:
首先需要知道:

$$\sum_{y_i=G_m(x_i)}\overline w_{mi}e^{-\alpha}=\sum_i^N \overline w_{mi}I(y_i=G(x_i)) tag{5.7} \\ \sum_{y_i≠G_m(x_i)}\overline w_{mi}e^{\alpha}≠\sum_i^N \overline w_{mi}I(y_i≠G(x_i) tag{5.8}$$

因此有:

$$\begin{align} \sum_{i=1}^N \overline w_{mi} e^{-y_i\alpha G(x_i))}&=\sum_{y_i=G_m(x_i)}\overline w_{mi}e^{-\alpha} +\sum_{y_i≠G_m(x_i)}\overline w_{mi}e^{-\alpha} \\ &=(e^\alpha-e^{-\alpha}) \sum_{i=1}^N \overline w_{mi}I(y_i≠G(x_i))+e^{-\alpha}\sum_{i=1}^N \overline w_{mi} \tag{5.9} \end{align}$$

将5.6带入5.9中,并对$\alpha$求导使导数为0,得到:

$$\alpha^*_m=\frac{1}{2}\log\frac{1-e_m}{e_m} \tag{5.10}$$

其中$e_m$使分类误差率:

$$e_m=\frac{\sum_i^N \overline w_{mi}I(y_i≠G_m(x_i))}{\sum_{i=1}^N \overline w_{mi}}=\sum_{i=1}^Nw_{mi}I(y_i≠G_m(x_i))$$

可以看出$\alpha_m$的更新和adaboost完全一致,最后再看样本权值的更新:

$$f_m(x)=f_{m-1}(x)+\alpha_mG_m(x) \tag{5.11}$$ $$\overline w_{m+1i}=e^{-y_if_m(x_i)} \tag{5.12}$$

将5.11带入5.12中得:

$$w_{m+1i}=\overline w_{mi}e^{-y_i\alpha_mG_m(x)}$$

与adaboost相比,只少了个规范化因子。