本文章只用于自己记录,详细内容好多博客已经讲的很清楚了。
参考博客1
参考博客2
参考博客3
参考平博客(最佳)
残差网络
我的实现
整体架构
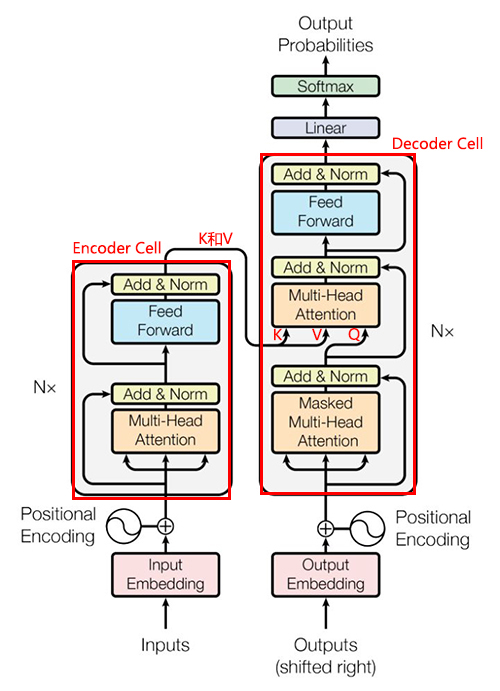
解释1:左半部分是encoder,方框中是一个encoder cell,右半部分是decoder,方框中是一个decoder cell。
解释2:一个encoder cell包含四层:self-Multi-Attention+ResNet And Norm+Feed-Forward+ResNet And Norm,名字和图中不太一样,按照层数数下即可.
解释3: 一个decoder cell包含六层:Mask-self-Multi-Attention+ResNet And Norm+encoder-decoder-Multi-Attention+ResNet And Norm+Feed-Forward+ResNet And Norm,名字和图中不太一样,按照层数数下即可.
解释4:encoder阶段的self-Multi-Attention和decoder阶段的Mask-self-Multi-Attention,encoder-decoder-Multi-Attention是同一段代码。
解释5:以翻译任务为例,假设当前需要翻译t位置的词汇,decoder阶段的mask-self-Attention是对0~t-1,即对已经翻译出来部分的attention,故需要做mask,防止attention未翻译部分,encoder-decoder-Attention是对原文所有的attention。
解释6:encoder-decoder-Multi-Attention并不是self-Attention,因为它的Q是原文状态,K和V是译文状态
self-Attention
先上图:
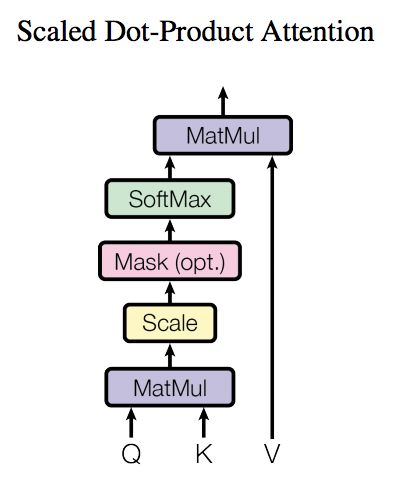
其实就是计算句子中每个单词对其他所有单词的关注程度:
这里只解释为啥要除以$\sqrt{dk}$:
除以$\sqrt{dk}$的意义
解释一
已知:
$axis=0$的意义是期望和方差都是指的$d_k$维向量的每个分量,且假设这$d_k$个分量独立同分布。目的是保持点积后期望方差不变。如果直接计算点积:$Q \times K^T$为$n \times n$维矩阵,注意,后面计算的期望和方差都是按照行或者列,不要想成整个矩阵的期望方差。以某个单词$q$为例($q_i$表示$q$的每个分量):
$E(qK^T)=E(\sum_0^{d_k}q_iK^T)=\sum_0^{d_k}E(K^T)=d_k \times 0=0$。其实把$q_i$看作一个常数即可
$D(qK^T)=D(\sum_0^{d_k}q_iK^T)=\sum_0^{d_k}D(K^T)=d_k \times 1=d_k$
而$D(\frac{qK^T}{\sqrt{d_k}})=D(qK^T)\times D((\frac{1}{d_k})^2)=d_k/d_k=1$
解释二
很简单的方法,一个$d_k$维的向量$q_i$,去乘以$d_k \times n$维度的向量,同时这个$d_k \times n$的向量在$d_k$的每个维度上(设第$i$个维度的随机变量为$X_i$)均值为零,方差为1,现在要求相乘后得到的向量,即一个$n$维向量的均值和方差,其实这和乘不乘$q_i$没关系,只和相乘的时候的加法有关系,最后$n$维度向量的均值$E=E(\sum_{i=0}^{d_k}X_i)=d_kE(X)=0$,同理$D(\sum_{i=0}^{d_k}X_i)=\sum_{i=0}^{d_k}D(X)=d_k$,因此要除以$\sqrt d_k$.
复杂度$O(n^2)$(n为序列长度)
三个步骤:
1.$Q \times K^T$,其实就是$n \times d_k$矩阵乘以$d_k \times n$维矩阵,复杂度是$O(d_kn^2)$
2.$softmax(Q \times K^T)$,没什么好说的,复杂度$O(n^2)$
3.$\frac{softmax(Q \times K^T)}{\sqrt{d_k}}$,就是一个$n\times d_k$矩阵乘以$d_k\times n$矩阵,复杂度$O(d_k^2 \times n)$
因此,去除常数$d_k$,复杂度就是$O(n^2)$
ResNet And Norm
残差网络的作用见残差网络,Norm的作用自然是加快收敛,防止梯度消失.
Feed-Forward
这里其实没有什么特殊的东西,源码中用了两个conv1,先把特征维度放大,在把特征维度缩小,其实也就是特征提取的作用.
Positional Encoding
由于在attention的时候仅仅计算了当前词与其他词的相关度,但是并没有其他词的位置信息,试想,输入一个待翻译的句子1,然后将该句中任意两个单词互换位置形成句子2,在当前结构中其实两个句子并没有什么不同,因此需要对每个单词引如其位置信息.在论文中使用的是这样的方式:
其中pos是当前单词在该句子中的位置,比如句子长20,则pos可以是1,2…20.i是在当前单词的第i个维度,比如每个单词有512个维度,则i可以是1,2…512.$d_{modle}$是单词维度,当前例子中即是512.
为什么要用三角函数呢?首先,这种方式能保证各个位置的位置信息各不相同。即绝对位置,其次,由
也就是说,如果单用sin和cos交替使用可以保证PE(pos+k)能用PE(pos)和PE(k)表示出来,也就是相对相对位置,如果仅仅使用sin或cos就没有了相对信息
进一步解释
对于一个序列,第$i$个单词和第$j$个单词的$Attention$ $score$为:
其中,$W_q$和$W_k$分别是$Q$和$K$的对齐权重,$E_i$和$E_j$分别是第$i$和$j$个单词的词向量,$U_i$和$U_j$分别是第$i$和$j$个单词的位置向量。
分解上式:
其中,只有$d$包含$i$和$j$的位置相对信息,我们知道:
如果没有$W_q$和$W_k$,则第$t$和词和第$t+k$个词的位置函数计算结果为:
发现如果没有$W_q$和$W_k$,位置距离为$k$的两个单词的同一维度只和相对位置有关,即包含了相对位置信息,但是加上这两个矩阵之后这种相对信息不复存在,但是在学习的过程中可以学出来,比如学到$W_qW_k=E$,这种相对位置信息就完全恢复了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
flag = 0
def attention_scores(d_model, t, k):
def get_angle(pos, i):
return pos / math.pow(10000, 2 * i / d_model)
angles1 = map(lambda x: get_angle(t, x), range(d_model // 2))
angles2 = map(lambda x: get_angle(t + k, x), range(d_model // 2))
result1 = list()
for angle in list(angles1):
result1.append(math.sin(angle))
result1.append(math.cos(angle))
result2 = list()
for angle in list(angles2):
result2.append(math.sin(angle))
result2.append(math.cos(angle))
result1 = np.asarray(result1)
result2 = np.asarray(result2)
if flag == 0:
return sum(result1 * result2)
elif flag == 1:
W1 = np.random.normal(size=(128, 256))
W2 = np.random.normal(size=(256, 128))
W = np.dot(W1, W2)
return sum(np.dot(result1.T, W) * result2)
else:
W = np.identity(128)
return sum(np.dot(result1.T, W) * result2)
if __name__ == '__main__':
result = list()
for pos in range(-50, 50):
result.append(attention_scores(d_model=128, t=64, k=pos))
data = pd.Series(result)
data.plot()
plt.show()
上诉代码表示第$64$个数据的位置向量和他前后各50个数据范围内的位置向量$attention$值 ,flag=0表示$U_t^T U_{t+k}$,flag=1表示$U_t^TWU_{t+k}$,flag=2表示$U_t^T E U_{t+k}$,$E$表示单位向量,运行代码可以看出flag=0/2图形对称有规律,flag=1图形毫无规律。
其他
1.每一个self-Attention都维护一个自己的$W_Q$,$W_K$,$W_V$,也就是生成Q,K,V的全连接神经网络参数,即每个cell的这三个值是不同的.
2.在encoder阶段的最后一个encoder cell会将生成的K和V传递给decoder阶段每个decoder cell的encoder-decoder-Multi-Attention使用.而encoder-decoder-Multi-Attention使用的Q是Mask-self-Multi-Attention输出的.
3.decoder阶段Mask-self-Multi-Attention用来Attention翻译过的句子,encoder-decoder-Multi-Attention用来Attention原文.
- 在代码中,的多头
Multi-Attention的实现实际上每个头把维度给均分了,并不是每个头都 attention 所有的维度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
self.depth = d_model // self.num_heads
self.wq = tf.keras.layers.Dense(d_model)
self.wk = tf.keras.layers.Dense(d_model)
self.wv = tf.keras.layers.Dense(d_model)
self.dense = tf.keras.layers.Dense(d_model)
def split_heads(self, x, batch_size):
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
q = self.wq(q) # (batch_size, seq_len, d_model)
k = self.wk(k) # (batch_size, seq_len, d_model)
v = self.wv(v) # (batch_size, seq_len, d_model)
q = self.split_heads(q, batch_size) # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size) # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
scaled_attention, attention_weights = self.scaled_dot_product_attention(q, k, v, mask)
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3])
concat_attention = tf.reshape(scaled_attention, (batch_size, -1, self.d_model))
output = self.dense(concat_attention) # (batch_size, seq_len_q, d_model)
return output, attention_weights
