总有一个算法让你惊艳

随机洗牌

问:一副牌54张，如何洗牌才能让最公平。
什么叫公平?就是每张牌在每个位置的概率都一样就是公平, Knuth 老爷子给出来这样的算法:

1. 初始化任意顺序
2. 从最后一张牌开始,设为第K张,然后从[1,K]张中任选一张与其交换
3. 从[1,K-1]张牌中任选一张和第K-1张交换... ...

伪代码:

1
2
3
4
for(int i =n;i>=1;i--)
{
    swap(array[i],random(1,i))
}

是不是贼简单？那为啥这个算法能做到呢？下面证明一下:
假设现在有5张牌，初始顺序为$1,2,3,4,5$
首先，从1~5(这是下标)中任选一张比如选到了2,那么用2和5交换得到$1,5,3,4,2$,也就是说，第一次交换2在最后一个位置的概率是1/5(也可以说任意一个数字在最后一个位置的概率是1/5),那么我们进行第二次交换,从1~4(这是下标)中任选一个和第4个交换,比如我们选到了1,在此之前要保证1没有在之前的步骤被选中也就是4/5,现在选中1的概率是1/4,那么两者相乘得到1/5,也就是1在第4个位置的概率是1/5也可以说任意一个数字在最后一个位置的概率是1/5),后面的不用多说了吧。
这题和蓄水池采样算法由异曲同工之妙。
用这个算法还可以在中途随意停止,比如有54张牌,我们要找任意10张牌进行公平洗牌,那么只需要上诉步骤执行10次就可以了.

轮盘赌随机算法

$\qquad$俄罗斯轮盘赌（Russian roulette）是一种残忍的赌博游戏。与其他使用扑克、色子等赌具的赌博不同的是，俄罗斯轮盘赌的赌具是左轮手枪和人的性命。俄罗斯轮盘赌的规则很简单：在左轮手枪的六个弹槽中放入一颗或多颗子弹，任意旋转转轮之后，关上转轮。游戏的参加者轮流把手枪对着自己的头，扣动板机；中枪的当然是自动退出，怯场的也为输，坚持到最后的就是胜者。旁观的赌博者，则对参加者的性命压赌注。
$\qquad$现在我们把问题抽象化，一个饼图，上面有一个指针，我们我们如何通过一个算法来确定到底每次拨动指针后会指向哪一个？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <ctime>
#include <vector>
#include <cstdlib>

using namespace std;

#define N  999 //精度为小数点后面3位

int RouletteWheelSelection()
{
    srand((unsigned) time(NULL));
    float m = rand() % (N + 1) / (float)(N + 1);
    cout << m << endl;
    float Probability_Total = 0;
    int Selection = 0;
    vector<float> Probabilities = {0.14, 0.35, 0.2, 0.07, 0.23, 0.01};
    for(int i = 0; i < Probabilities.size(); i++)
    {
        Probability_Total += Probabilities[i];
        if(Probability_Total >= m)
        {
            Selection = i;
            break;
        }
    }
    return Selection;
}

int main()
{
    cout << RouletteWheelSelection();
    return 0;
}

其实只要意识到需要最终各部分的概率与占比相同即可。

切分句子

在NLP中经常会有这样的需求,对于训练数据有少部分会特别长,远远超出平均长度,那么我们就需要对句子进行拆分,但是不能直接安长度切，这样很可能会切断关键词,切分方法一般是在无用的地方切分,比如标点符号,现在给出一个算法实现这个功能:

1
2
3
4
5
6
7
8
9
10
11
12
def data_cut(sentence, cut_chars, cut_length, min_length):
    if len(sentence) <= cut_length:
        return [sentence]
    else:
        for char in cut_chars:
            start = min_length  # 防止直接从头几个就找到了，这样切的太短
            end = len(sentence) - (min_length - 1)  # 防止从最后几个找到了,这样切的也太短
            if char in sentence[start:end]:
                index = sentence[start:end].index(char)
                return data_cut(sentence[:start + index], cut_chars, cut_length, min_length) + \
                       data_cut(sentence[start + index:], cut_chars, cut_length, min_length)
    return [sentence]  # 如果没有找到切分点那就不管句子长度直接返回

>
参数说明:sentence是一个list,内容是sentence每个字符
cut_chars是一个list,内容是切分字符，按优先级排序
cut_length是int类型，表示切分多长的句子,这个长度以及以下的直接返回
min_length:切分后子句子的最短长度
return:二维list,注意，每个切分后的句子不一定全小于cut_length,有些另类的句子可能没有切分点,这样的需要手动处理
eg:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def data_cut(sentence, cut_chars, cut_length, min_length):
    if len(sentence) <= cut_length:
        return [sentence]
    else:
        for char in cut_chars:
            start = min_length
            end = len(sentence) - (min_length - 1)
            if char in sentence[start:end]:
                index = sentence[start:end].index(char)
                return data_cut(sentence[:start + index], cut_chars, cut_length, min_length) + data_cut(
                    sentence[start + index:], cut_chars, cut_length, min_length)
    return [sentence]


if __name__ == '__main__':
    sentence = "三种上下文特征：单词、n-gram 和字符在词嵌入文献中很常用。大多数词表征方法本质上利用了词-词的共现统计，即使用词作为上下文特征（词特征）。受语言建模问题的启发，开发者将 n-gram 特征引入了上下文中。词到词和词到 n-gram 的共现统计都被用于训练 n-gram 特征。对于中文而言，字符（即汉字）通常表达了很强的语义。为此，开发者考虑使用词-词和词-字符的共现统计来学习词向量。字符级的 n-gram 的长度范围是从 1 到 4（个字符特征）。"
    l = data_cut(list(sentence), ['，', '。'], 150, 5)
    print(l)
#自己运行看看吧，不好写

约瑟夫环

n个人拉成圈，按照1~n标号,从1开始报数,报到m的人出局，每一次有人出局后重新排号，1号是重新排号前m的下一个人.

1
2
3
4
5
int JosephRing(int n, int m)
{
    if (n == 1) return n;
    return (JosephRing(n - 1, m) + m - 1) % n + 1;
}

解释:对于任何一个状态而言，每个位置设为$old_i$,如果现在把该状态的第$m$个剔除掉，则重新排号后每个位置设为$new_i$,两者的关系

$JosephRing(n,m)$表示有$n$个人,每次删除$m$号人最终剩下的号码，每次递归回来其实都是再算

点和线

一个知识点

定义: 平面上的三点$A(x1,y1),B(x2,y2),C(x3,y3)$的面积量:

其中: 当A、B、C逆时针时S为正的,反之S为负的。
证明如图: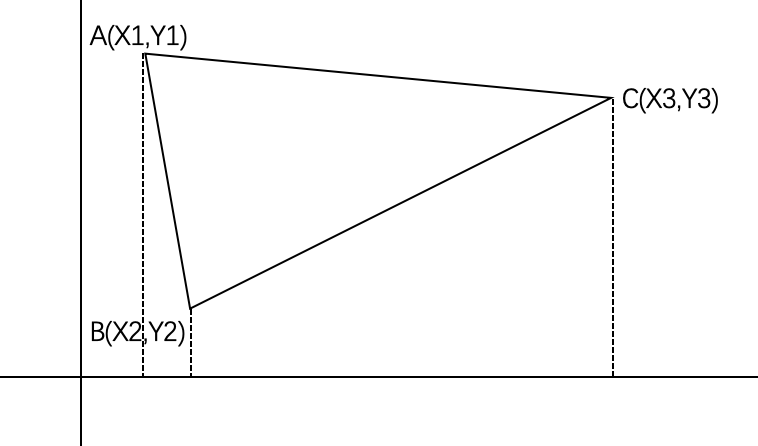


也就是说，平面三点一定能写成一个直角梯形减两个直角三角形的形式.
即:

正好是上诉行列式.

一个应用

令矢量的起点为A，终点为B，判断的点为C，
如果S(A，B，C)为正数，则C在矢量AB的左侧；
如果S(A，B，C)为负数，则C在矢量AB的右侧；
如果S(A，B，C)为0，则C在直线AB上

点和矩形

判断坐标系内某电点是否在某个矩形内部

只需要将点与四个角连接，计算形成的四个三角形面积(海伦公式)和是否等于矩形面积,等于则在内部，否则在外部。

判断平面内两线段相交

  1. 计算两线段所在的直线的的交点(如果有),然后看该交点是否在两条线段上即可
  2. 若两直线相交,则如图:,,,算了不弄图了，也简单，假设有线段AB 和 CD 若相交则必定C 和 D 在 AB 的两侧，则有$\vec{AB} \times \vec{AC} $和$\vec{AB} \times \vec{AD} $必定异号 $\vec{AB} \times \vec{AC} $和$\vec{CA} \times \vec{CD} $必定异号，判断这个即可