神经网络到底保存了什么

都知道，无论使用什么框架，神经网络都是非常消耗显存的，那么，这些消耗的显存到底保存了什么？

从一个例子开始

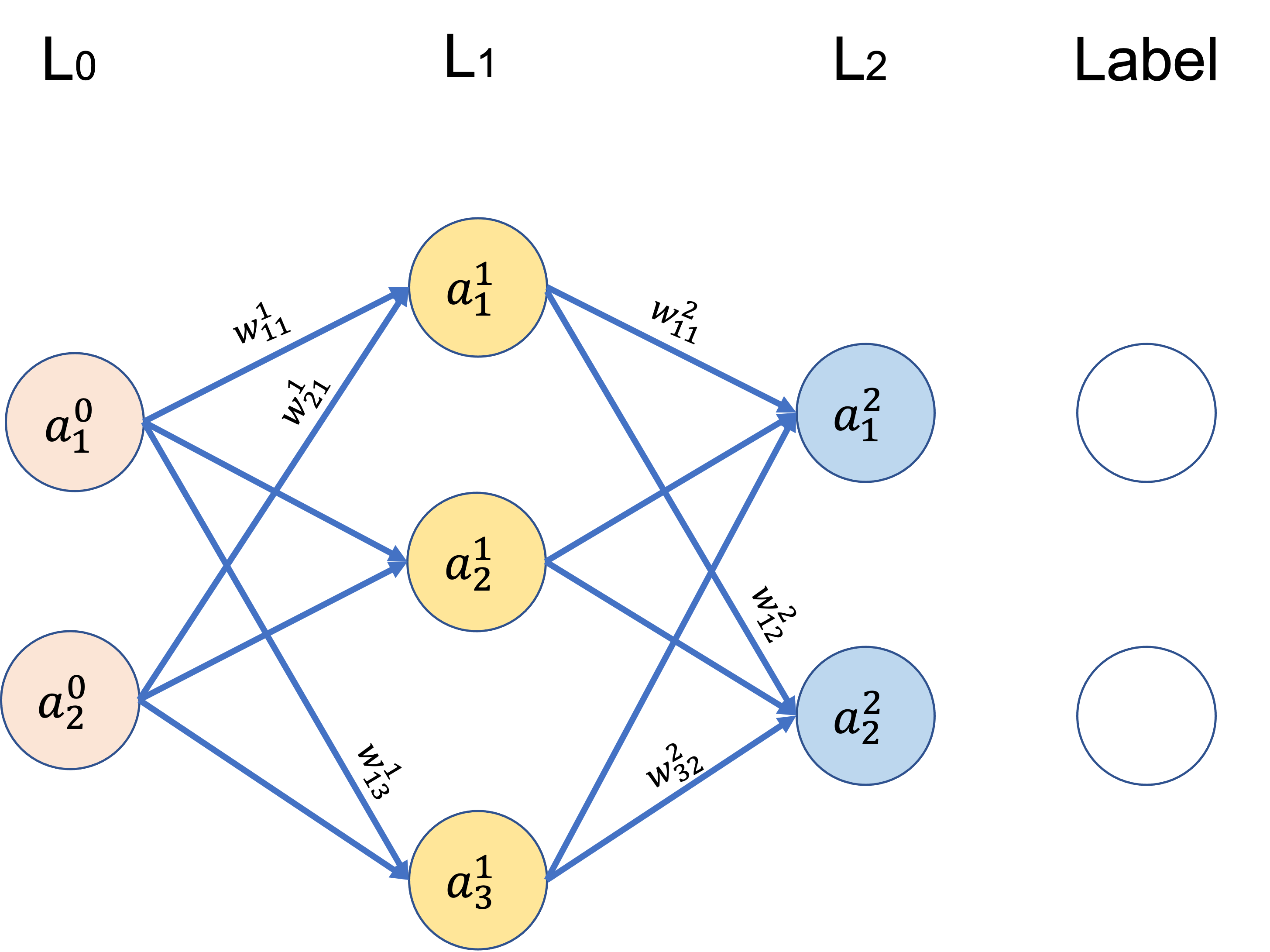
标注解释:
$z_i^k$:第$k$层第$i$个$feature$的输出(不经过激活函数))
$a_i^k$：其值为$g(z_i^k)$,$g(x)$为激活函数，这里把输入层数据$x_i$看作第0层。
$w_{ij}^k$: 从第$k-1$层到第$k$层的传播权重
这里去掉了偏置权重$b$

正向传播:

$$\left\{ \begin{aligned} z_1^1=w_{11}^1a_1^0+w_{21}^1a_2^0 \\ z_2^1=w_{12}^1a_1^0+w_{22}^1a_2^0 \\ z_3^1=w_{13}^1a_1^0+w_{23}^1a_2^0 \end{aligned} \right. \tag{1}$$ $$a_i^1=g(z_i^1) \tag{2}$$ $$\left\{ \begin{aligned} z_1^2=w_{11}^2a_1^1+w_{21}^2a_2^1+ w_{31}^2a_3^1\\ z_2^2=w_{12}^2a_1^1+w_{22}^2a_2^1+ w_{32}^2a_3^1\\ \end{aligned} \right. \tag{3}$$ $$a_i^2=g(z_i^2) \tag{4}$$

反向传播

假设损失函数为MSE损失:

$$Loss=\frac{1}{2}\sum_{i=0}^n(y_i-a_i^2)^2 \tag{5}$$

下面开始计算对各个参数$w_{ij}^k$的偏导。
从最近的开始:

$$\left\{ \begin{aligned} \frac{\partial L}{\partial w_{11}^2}= \frac{\partial L}{\partial z_1^2} \frac{\partial z_1^2}{w_{11}^2}=\frac{\partial L}{\partial z_1^2} a_1^1 \\ \frac{\partial L}{\partial w_{21}^2}= \frac{\partial L}{\partial z_1^2} \frac{\partial z_1^2}{w_{21}^2}=\frac{\partial L}{\partial z_1^2} a_2^1 \\ \frac{\partial L}{\partial w_{31}^2}= \frac{\partial L}{\partial z_1^2} \frac{\partial z_1^2}{w_{31}^2}=\frac{\partial L}{\partial z_1^2} a_3^1 \\\\ \frac{\partial L}{\partial w_{12}^2}= \frac{\partial L}{\partial z_2^2} \frac{\partial z_2^2}{w_{12}^2}=\frac{\partial L}{\partial z_2^2} a_1^1 \\ \frac{\partial L}{\partial w_{22}^2}= \frac{\partial L}{\partial z_2^2} \frac{\partial z_2^2}{w_{22}^2}=\frac{\partial L}{\partial z_2^2} a_2^1 \\ \frac{\partial L}{\partial w_{32}^2}= \frac{\partial L}{\partial z_2^2} \frac{\partial z_2^2}{w_{32}^2}=\frac{\partial L}{\partial z_3^2} a_3^1 \end{aligned} \right. \tag{6}$$ $$\left\{ \begin{aligned} \frac{\partial L}{\partial w_{11}^1}= \frac{\partial L}{\partial z_1^1} \frac{\partial z_1^1}{\partial w_{11}^1}=\frac{\partial L}{\partial z_1^1} a_1^0 \\ \frac{\partial L}{\partial w_{21}^1}= \frac{\partial L}{\partial z_1^1} \frac{\partial z_1^1}{\partial w_{21}^1}=\frac{\partial L}{\partial z_1^1} a_2^0 \\\\ \frac{\partial L}{\partial w_{12}^1}= \frac{\partial L}{\partial z_1^1} \frac{\partial z_2^1}{\partial w_{12}^1}=\frac{\partial L}{\partial z_2^1} a_1^0 \\ \frac{\partial L}{\partial w_{22}^1}= \frac{\partial L}{\partial z_2^1} \frac{\partial z_2^1}{\partial w_{22}^1}=\frac{\partial L}{\partial z_1^1} a_2^0 \\\\ \frac{\partial L}{\partial w_{13}^1}= \frac{\partial L}{\partial z_3^1} \frac{\partial z_3^1}{\partial w_{13}^1}=\frac{\partial L}{\partial z_3^1} a_1^0 \\ \frac{\partial L}{\partial w_{23}^1}= \frac{\partial L}{\partial z_3^1} \frac{\partial z_3^1}{\partial w_{23}^1}=\frac{\partial L}{\partial z_3^1} a_2^0 \end{aligned} \right. \tag{7}$$

由公示(6)(7)可以总结出来:

$$\frac{\partial L}{\partial w_{ij}^k}=\frac{\partial L}{\partial z_j^k}a_i^{k-1} \tag{8}$$

其中$a_i^{k-1}$在正向传播中已经算出，下面计算$\frac{\partial L}{\partial z_j^k}$:

$$\left\{ \begin{aligned} \frac{\partial L}{\partial z_1^2}=\frac{\partial L}{\partial a_1^2}g'(z_1^2) \\ \frac{\partial L}{\partial z_2^2}=\frac{\partial L}{\partial a_2^2}g'(z_2^2) \end{aligned} \right. \tag{9}$$ $$\left\{ \begin{aligned} \frac{\partial L}{\partial z_1^1}=\frac{\partial L}{\partial a_1^1}g'(z_1^1)=(\frac{\partial L}{\partial z_1^2}w_{11}^2+\frac{\partial L}{\partial z_2^2}w_{12}^2)g'(z_1^1) \\ \frac{\partial L}{\partial z_2^1}=\frac{\partial L}{\partial a_2^1}g'(z_2^1)=(\frac{\partial L}{\partial z_1^2}w_{21}^2+\frac{\partial L}{\partial z_2^2}w_{22}^2)g'(z_2^1) \\ \frac{\partial L}{\partial z_3^1}=\frac{\partial L}{\partial a_3^1}g'(z_3^1)=(\frac{\partial L}{\partial z_1^2}w_{31}^2+\frac{\partial L}{\partial z_2^2}w_{32}^2)g'(z_3^1) \end{aligned} \right. \tag{10}$$

由(9)(10)可知，要求得$\frac{\partial L}{\partial z_j^k}$，需要$w_{ij}^k$和$z_i^k$。

总结

$\qquad$现在可以得出结论，在整个神经网络训练过程中，出于反向传播的需要，我们需要在正向传播的时候在显存中记录$a_i^k$、$w_{ij}^k$和$z_i^k$。但是由于我们常用的激活函数都是可逆的，即知道$a_i^k$能反算出$z_i^k$，因此也可以只保存$a_i^k$、$w_{ij}^k$。