立题依据

研究意义

Transformer^[1]从2017年被提出至今，一直是NLP领域重点研究对象，各种SOTA模型的诞生几乎都离不开它的加持，如今甚至在NLP领域已经成为标配，有完全取代CNN和RNN的趋势，在CV领域也有席卷的迹象。尽管Transformer^[1]取得这么大成功，但是它有一个致命缺陷，其时空复杂度均为$O(n^2)$,其中$n$代表序列长度,这也是限制其在CV领域发展的一个重要原因，正因如此，不少工作被迫妥协，经典模型Bert^[2]最长长度只有512，对于短文本而言还可以接受，但对长文本例如一篇文章一般几千个token，这种长度的序列直接训练会导致显存不足因此只能被迫截断，这样必然损失精度，因此研究如何降低复杂度至关重要。

国内外研究现状

针对Transformer^[1]时空复杂度过大的问题，业内已经有研究人员提出提出一些解决方案，Qipeng Guo等人提出Star-Transformer^[3]，将密集Attention结构改为星形结构，基本思想是将计算两两token之间注意力分数改为计算各个token和中心token的注意力分数，从而降低复杂度。Rewon Child等人提出Sparse Transformer^[4]，基本思路是对于某个token而言，只需要计算对其贡献最大的若干个注意力分数即可，通过将Transformer模型中的Attention矩阵稀疏化来达到减少内存消耗、降低计算力的方法，基本做法是在Softmax阶段只保留topK个结果，将计算复杂度从$O(n^2)$降低到$O(n^\frac{2}{3})$.Zihao Ye等人提出BP-Transformer^[5]，采用分治法利用多层二叉树，逐步计算Attention最终归并，将计算复杂度降低到$O(n\log n)$。 Iz Beltagy等人提出Longformer^[6]，对于每一个token只对固定窗口大小附近的token进行Local Attention，同时附近token采用了类似空洞卷积的方式增强用来捕获更长的序列长度的信息，针对特定任务的特定token做Global Attention，但值得注意的是，在原始代码中所谓的Local Attention窗口大小也达到了512,即内存量和Bert^[2]相比并没有减少。Zihang Dai等人提出Transformer-XL^[7],将长文档切块，从第一个块开始做Transformer，然后以模仿RNN的方式传递到下一个块递归的训练，该方案被用在很多其他工作中，例如Xlnet^[8]，同时XlNet^[8]也使用了一种全排列的乱序方式，但是该乱序中加入了位置信息，不能算真正乱序。Sainbayar Sukhbaatar等人提出自适应跨度 Transformer^[9]，主要思想是抛弃了区域Attention固定窗口的做法，使用一种能自适应选择长下文窗口大小的方案。Nikita Kitaev等人提出Reformer^[10]，选择通过局部敏感哈希技术将每个词例的注意力范围变窄，Aurko Roy 等人提出Routing Transformer^[11]尝试将问题建模为了一个路由问题，从而让模型学会选择词例的稀疏聚类。Siyu Ding等人在ERNIE-DOC^[12]中提出回溯式feed机制和增强的循环机制，其基本原理是对于一篇长文，采用先略读后精读的方式，其中回溯式feed机制参考了xlnet^[8]通过粗细两种粒度从乱序恢复正常语序，增强的循环机制借鉴了Transformer-xl^[7]，但是将上一时刻上一层的输出改为上一时刻下一层的输出，相当于扩大感受野。

研究方案

研究目标、研究内容和关键问题

研究目标

本论文的研究目标是提出并实现一种双层Self-Attention结构的Transformer，用于降低普通Transformer时空复杂度。

研究内容

普通的Transformer模型时间和空间复杂度都是$O(n^2)$,需要注意的是这里的复杂度指的是乘/除法运算的复杂度,证明如下：

$Attention(Q_{n\times d_k},K_{n\times d_k},V_{n\times d_k})=\frac{softmax(Q_{n\times d_k}\times K_{n\times d_k}^T)}{\sqrt{d_k}} \times V_{n\times d_k}$

第一步: $Q_{n\times d_k}\times K_{n\times d_k}^T$乘法计算量为$d_k\times n^2$.

第二步:$softmax(Q_{n\times d_k}\times K_{n\times d_k}^T)$乘法计算量为$n^2$.

第三步:$\frac{softmax(Q_{n\times d_k}\times K_{n\times d_k}^T)}{\sqrt{d_k}}$除法计算量为$d_k\times n^2$.

第四步:$\frac{softmax(Q_{n\times d_k}\times K_{n\times d_k}^T)}{\sqrt{d_k}} \times V_{n\times d_k}$乘法计算量为$d_k\times n^2$.

综上所述，去除常数$d_k$，可得复杂度为$O(n^2)$,如此大的复杂度在面对长文本时很难处理，时间上勉强可以接受，但是空间上很难解决，通常只能通过限制文本长度或减小batchsize来解决，此方式过于暴力，无疑会增加降低模型效果，本论文拟尝试一种双层self-Attention的Transformer模型，其基本结构如下：

双层self-Attention

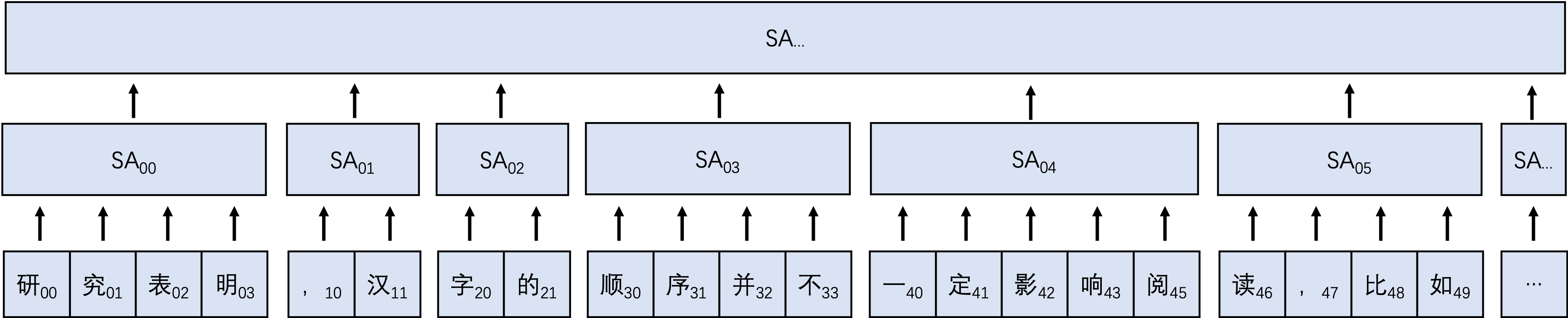
基本思想是对长序列进行分块，先通过块内计算Attention Score，然后通过块间计算全局Attention Score。图中$token_{ij}$中$i$表示第$i$个块,$j$表示块中第$j$个token，$SA_{ij}$表示第$i$层第$j$个块的$SA$。

关键问题

如何设置各个分块大小？
常见方式是固定窗口大小，本论文拟尝试的方式如下：
固定分区后分块数量$m$，则平均每个块长度为$\frac{n}{m}$,然后每个块实际大小设置为$r_i=random[1,\frac{2n}{m}]$，且满足$\sum_ir_i=n$。之所以希望窗口大小随机而不是固定主要是考虑希望窗口在序列的位置信息不是固定位置而是一定范围的位置。
按照标准Transformer，backbone需要串联起来，但是上诉方式，第一层backbone之后序列长度就和之前不一样了，无法直接衔接到相同形状的下一层，在BP-Transformer中解决该问题的方案是用根节点去做类似分类任务，用叶子结点去做生成任务，但是叶子是处于第一层，理论上越深层语义信息越丰富，经典论文Transformer中做翻译任务用的就是Encoder的最后一层。本论文中该问题拟尝试的解决方案有两个:

方案一：基本思路是为使每一个backbone输入输出相同，可尝试将两层Attention结合，即第一层SA用于捕获块内注意力，第二层SA用于捕获全局注意力，然后两者拼接即可恢复输入形状，进而可以随意串联，同时每一个backbone会重新分块。该方式可以用于任何任务。

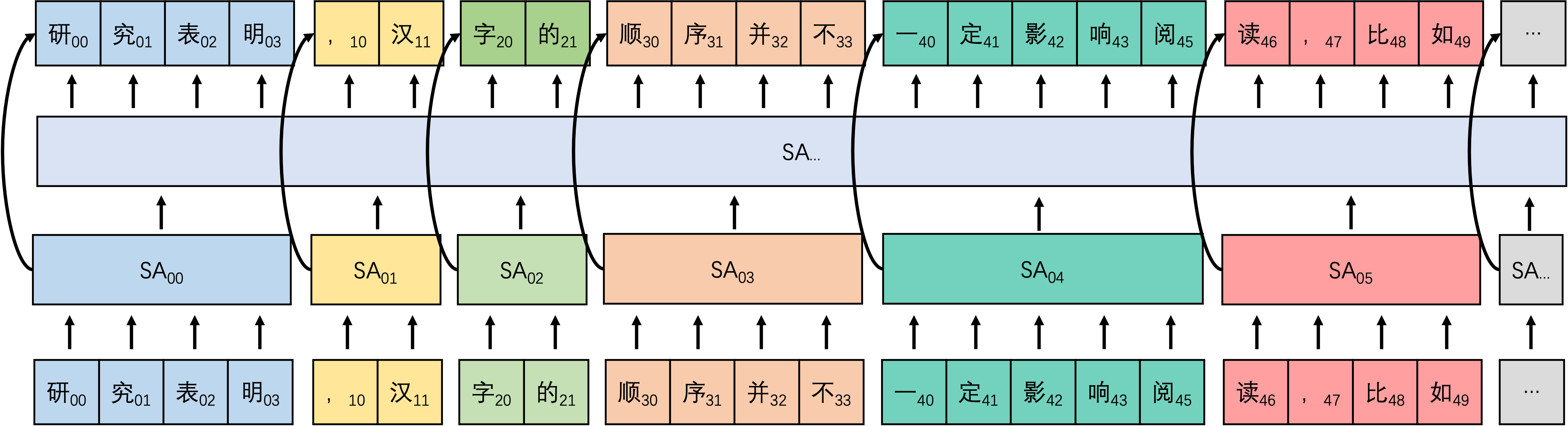
堆叠self-Attention
方案二：基本思路是类似多层cnn堆叠的方式，呈现金字塔形状，同时并行训练多个不同分块方式的相同模型，最后一层concat在一起，该方式可用于多对一的任务中。

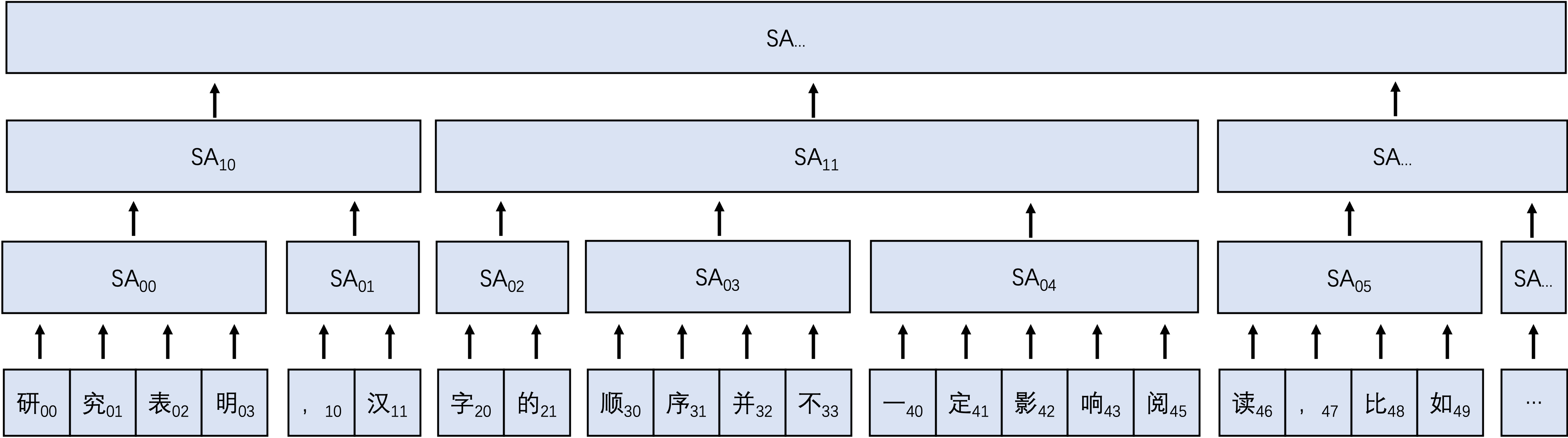
金字塔self-Attention

SA数量的增多也意味着FNN数量的增多，可能会增加参数：
可以尝试同层同形SA之间参数共享。
块内位置信息是否必要？
在Nlp领域无论什么任务都比较强调语序，因此一般都会加上位置信息，看起来很正常，但一定要如此么？有个传播已久例子：“研表究明，汉字的序顺并不定一能影阅响读，比如当你看完这句话后，才发这现里的字全是乱的。”但是如果我们把这句话改为：”影研明字，的序究顺并表不当一汉阅响，比读现你看完发这定话后，才这里能的字全是如句乱的。”正常情况下很难一眼理解句意，看起来有趣的同时也蕴含着一定的道理，语序确实很重要，但或许不是那么重要？
出于这种思考，本论文拟尝试一种区域内乱序的方案，意思是分块后块之间严格语序，但是块内不严格语序。基本结构可以参考双层self-Attention图，并将第一层SA改为reduce_sum/reduce_mean即可实现块内乱序。

可行性分析

本小节旨在证明该方法是否能够降低复杂度，以及最优复杂度是多少。

命题

假设一段文字长度为$n$，则其在self-Attention部分计算量为$n^2$，我们把它切成$m$段，为方便计算假设每段长度相同,即$\frac{n}{m}$，求此时双层self-Attention的计算量最低是多少。

解题

根据上图可得则此时的计算量为:$\frac{n^2}{m^2} \times m + m^2=\frac{n^2}{m}+m^2$(块内Attention和块间Attention相加)，令：

$f(m)=\frac{n^2}{m}+m^2 \quad (1<m<n)$

求导：

$f'(m)=\frac{2m^3-n^2}{m^2}\quad (1<m<n)$

令$f’(m)=0$,求得$m=(\frac{n^2}{2})^\frac{1}{3}$,$f(m)$在$(1,(\frac{n^2}{2})^\frac{1}{3}]$为减函数，$[(\frac{n^2}{2})^\frac{1}{3},n)$为增函数，因此$m=(\frac{n^2}{2})^\frac{1}{3}$时可求得$f(m)$最小值$n^{\frac{4}{3}}\times(2^{\frac{1}{3}}+2^{-\frac{2}{3}})=\frac{3n^\frac{4}{3}}{2^\frac{2}{3}}$,复杂度为$O(n^{4/3})$。
和Bert对比，假设n=512,则原始计算量为262144，而双层self-Attention当m=50时，计算量最优值仅为7740,远远小于262144。理论上如果和普通Bert相同的计算量，双层self-Attention可处理序列长度为7500，远大于512。
虽然从复杂度上看，$O(n^{4/3})$和$O(n^2)$差不了很多，但是从计算量角度还是有一定的效果，当然理论上self-Attention层越多越能减轻计算负担。

创新点

本文尝试提出一种利用双层self-Attention降低Transformer复杂度的方案，利用块内自注意力和块间自注意力的结合，将普通Transformer自注意力机制的复杂度从$O(n^2)$降低到$O(n^\frac{4}{3})$。

研究计划

参考文献

双层自注意力Transformer

2021-11-13

双层自注意力Transformer

立题依据

研究意义

国内外研究现状

研究方案

研究目标、研究内容和关键问题

研究目标

研究内容

关键问题

可行性分析

命题

解题

创新点

研究计划

参考文献

双层自注意力Transformer

立题依据

研究意义

国内外研究现状

研究方案

研究目标、研究内容和关键问题

研究目标

研究内容

关键问题

可行性分析

命题

解题

创新点

研究计划

参考文献

谢谢~~