word2vec

本文不作为详细教程，知识自己容易遗忘知识点的记录。

语言模型

通俗来说就是用来量化哪个句子更像人话的模型,目前可分为统计语言模型和神经网络模型。

统计语言模型

由Bayes公式,一个句子组成的概率公式为:

$$p(w_k|w_1^{k-1})=\frac{p(w_1^k)}{p(w_1^{k-1})} \tag{1}$$

根据大数定理:

$$p(w_k|w_1^{k-1})≈\frac{count(w_1^k)}{count(w_1^{k-1})} \tag{2}$$

由马尔科夫假设:任意一个词出现的概率只是他前面出现的有限的一个或者几个词相关(未来的事件，只取决于有限的历史)
基于马尔可夫假设，N-gram 语言模型认为一个词出现的概率只与它前面的n-1个词相关,即:

$$p(w_k|w_{k-n+1}^{k-1})=\frac{p(w_{k-n+1}^k)}{w_{k-n+1}^{k-1}}≈\frac{count(w_{k-n+1}^k)}{count(w_{k-n+1}^{k-1})} \tag{3}$$

eg:
n=2

$$p(w_k|w_{k-1})≈\frac{count(w_{k-1}^{k})}{count(w_{k-1})} \tag{4}$$

一般而言,语言模型利用最大似然确定目标函数(即最大化某句子的概率):

$$Loss=\sum_w \log p(w|context(w)) \tag{5}$$

其中:

$$p(w|context(w))=F(w,context(w),\theta) \tag{6}$$

比如早期的智能ABC据说就是用的N-gram,还有搜索引擎,输入一个词后面多个选项也是N-gram.

神经网络语言模型

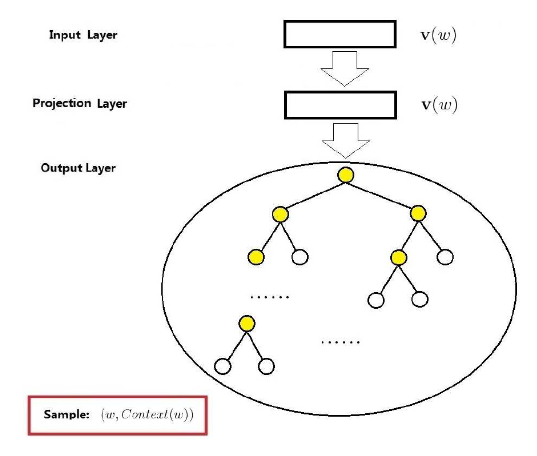
神经概率语言模型(NPLM)

该结构是词向量模型的先驱
网络结构: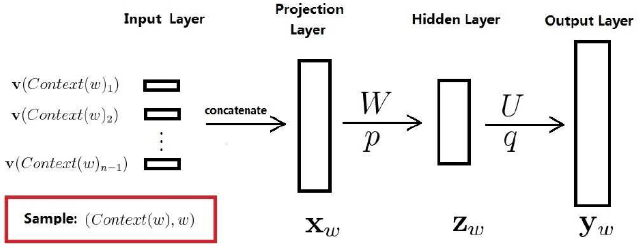

• Input Layer是n-1个词的词向量首尾相连,得到$x_w$,长度为:$(n-1)m$,$m$是词向量长度.
• Projectjon Layer是:$z_w=tanh(Wx_w+p)$,长度依然为$(n-1)m$.
• Hjdden Layer是$y_w=Uz_w+q$,得到的$y_w=(y_1,y_2…y_N)$,N是词表大小.
• Output Layer是$softmax$,即将$y_w$的各个分量做$softmax$，使其加和为1.

由式(6)$F(w,context(w),\theta)$,此时$\theta$包含:

• 词向量: $v_w\in R^m$
• 神经网络参数: $W \in R^{n_h \times (n-1)m},p \in R^{n_h},Y \in R^{n_h},q \in R^{N}$
  其中$n_h$是batchsjze,N是词典大小。

词向量模型

基于Hierarchical SoftMax

CBOW

由上下文词推断当前词的词向量模型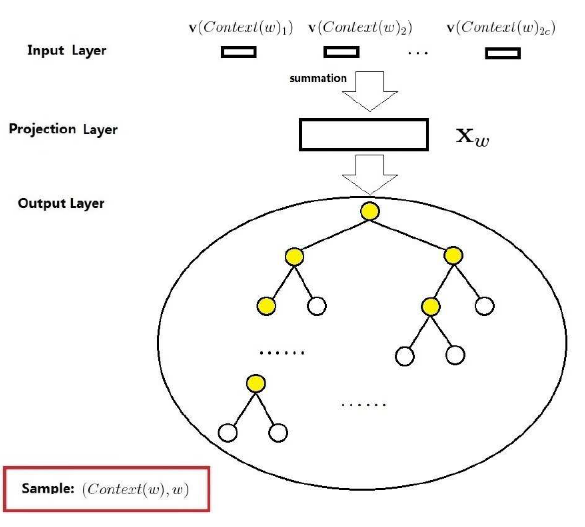

• Input Layer: $2c$个词的随机初始化词向量
• Projectjon Layer是:$x_w=\sum_{j=1}^{2c}v(context(w)_j)$
• Output Layer:是一颗由训练语料构成的Huffman树

与NPML相比,他们的$x_w$不同,NPML是收尾相接,而$CBOW$是向量加和.他们的输出层不同,NPML是输出层是线性结构,$CBOW$输出层是$Huffman$树.
损失函数计算:
引入一些符号:

• $p^w$:从根节点到达$w$节点的路径
• $l^w$:路径$p^w$中节点的个数
• $p^w1…p^w{l^w}$:依次代表路径中的节点,根节点-中间节点-叶子节点
• $d2^w…d^w{l^w} \in {0,1}$:词$w$的$Huffman$编码,由$l^w-1$位构成,根节点无需编码
• $\theta1^w…\theta^w{l^w-1}$: 路径中非叶子节点对应的向量,用于辅助计算。
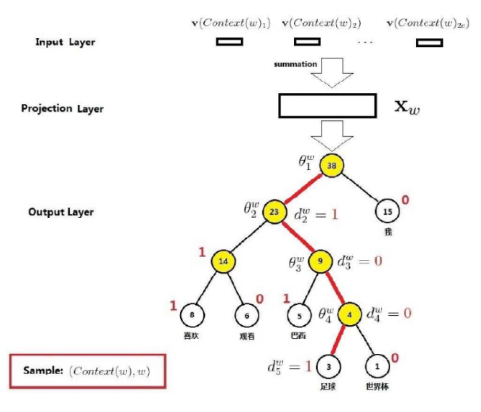
• 单词$w$是足球,对应的上下文词汇为$c_w$,上下文词向量和为$x_w$
  举例说明:

  

  约定编码1为负类,0为正类,每一个节点就是一个二分类器，是逻辑回归(sjgmojd)。其中$\theta$
  是对应的非叶子节点的向量，一个节点被分为正类和负类的概率分别如下: $$\sigma(x^T_w\theta)=\frac{1}{1+e^{x^T_w\theta}},1-\sigma(x^T_w\theta)$$ 那么从根节点到足球的概率为:

1. 第一次: $p(d_2^w|x_w,\theta_1^w)=1-\sigma(x_w^T\theta_1^w)$
2. 第二次: $p(d_3^w|x_w,\theta_2^w)=\sigma(x_w^T\theta_2^w)$
3. 第三次: $p(d_4^w|x_w,\theta_3^w)=\sigma(x_w^T\theta_3^w)$
4. 第四次: $p(d_5^w|x_w,\theta_4^w)=1-\sigma(x_w^T\theta_4^w)$ $$p(足球|c_{足球})=\prod_{j=2}^5p(d_j^w|x_w,\theta_{j-1}^w)$$ 该公式即为目标函数,重新整理: $$p(w|context(w))=\prod_{j=2}^{l^w}p(d_j^w|x_w,\theta_{j-1}^w)$$ 其中 $$p(d_j^w|x_w,\theta_{j-1}^w) = \begin{cases} \sigma(x_w^T\theta_{j-1}^w) & d_j^w=0\\ 1-\sigma(x_w^T\theta_{j-1}^w) & d_j^w=1\\ \end{cases}$$ 写成整体形式为: $$p(d_j^w|x_w,\theta_{-1}^w)=[\sigma(x_w^T\theta_{j-1}^w)]^{1-d_j^w}·[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}$$ 最大似然损失函数 $$\begin{align} L &= \sum_{w \in C} \log \prod_{j=2}^{l^w}\{[\sigma(x_w^T\theta_{j-1}^w)]^{1-d_j^w}·[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}\}\\ &= \sum_{w \in C}\sum_{j=2}^{l^w}\{(1-d_j^w)·log[\sigma(x_w^T\theta_{j-1}^w)]+d_j^w·log[1-\theta(x_w^T\theta_{j-1}^w)]\} \end{align}$$ 令$L(w,j)=\sum{w \in C}\sum{j=2}^{l^w}{(1-dj^w)·log[\sigma(x_w^T\theta{j-1}^w)]+dj^w·log[1-\theta(x_w^T\theta{j-1}^w)]}
   $
   则 $$L=\sum_{w \in C}L(w,j)$$ 对于具体求导见参考1和参考2

   Skip-Gram

   由上下文词推断当前词的词向量模型

   

• Input Layer:中心词w的词向量$v_w$
• Projectjon Layer:其实在这里是多余的，只是为了和CBOW做对比
• Output Layer:是一颗由训练语料构成的Huffman树
  由于需要预测中心词左右共2c个词，因此每次预测都需要走2c遍该Huffman树(CBOW)只需要走一遍，因此条件概率应为: $$p(Context(w)|w)=\prod_{u \in Context(w)} p(u|w)$$ 而 $$p(u|w)=\prod_{j=2}^{l^u}p(d_j^u|v_w,\theta_{j-1}^u)$$ 上诉公式仿照CBOW即可 $$p(d_j^u|v_w,\theta_{-1}^u)=[\sigma(v_w^T\theta_{j-1}^u)]^{1-d_j^u}·[1-\sigma(v_w^T\theta_{j-1}^u)]^{d_j^u}$$ 根据最大似然估计得: $$\begin{align} L &=\sum_{w \in c} log \prod_{u \in Context(w)} \prod_{j=2}^{l^u}\{[\sigma(v_w^T\theta_{j-1}^u)]^{1-d_j^u}·[1-\sigma(v_w)^T\theta_{j-1}^u]\} \\ &= \sum_{w \in C} \sum_{u \in Context(w)} \sum_{j=2}^{l^u}\{(1-d_j^u)·log[\sigma(v_w)^T\theta_{j-1}^u]+d_j^u·log[1-\sigma(v_w)^T\theta_{j-1}^u]\} \end{align}$$ 令 $$L(w,u,j)=(1-d_j^u)·log[\sigma(v_w)^T\theta_{j-1}^u]+d_j^u·log[1-\sigma(v_w)^T\theta_{j-1}^u]$$ 求梯度同上

  基于Negative Sampling

个人想法

对于cbow的hierarchical softmax伪代码:

Negative Sampling伪代码:

我觉得大多数博客说的hierarchical softmax一次更新所有参数的说法简直误人子弟,看看伪代码即可,hierarchical softmax一次性更新的权重是该路径上所有非叶子节点的权值,因此如果huffman数很大,则更新的权值也就非常多,而Negative Sampling的方式只更新正样本对应的一个权值和负样本对应各自的权值,是固定个数的,所以它更新的权值少。