Tensorflow中Rnn的实现

包含TensorFlow中BasicRNNCell,BasicLSTMCell等的实现

1.BasicRNNCell
基本结构如图: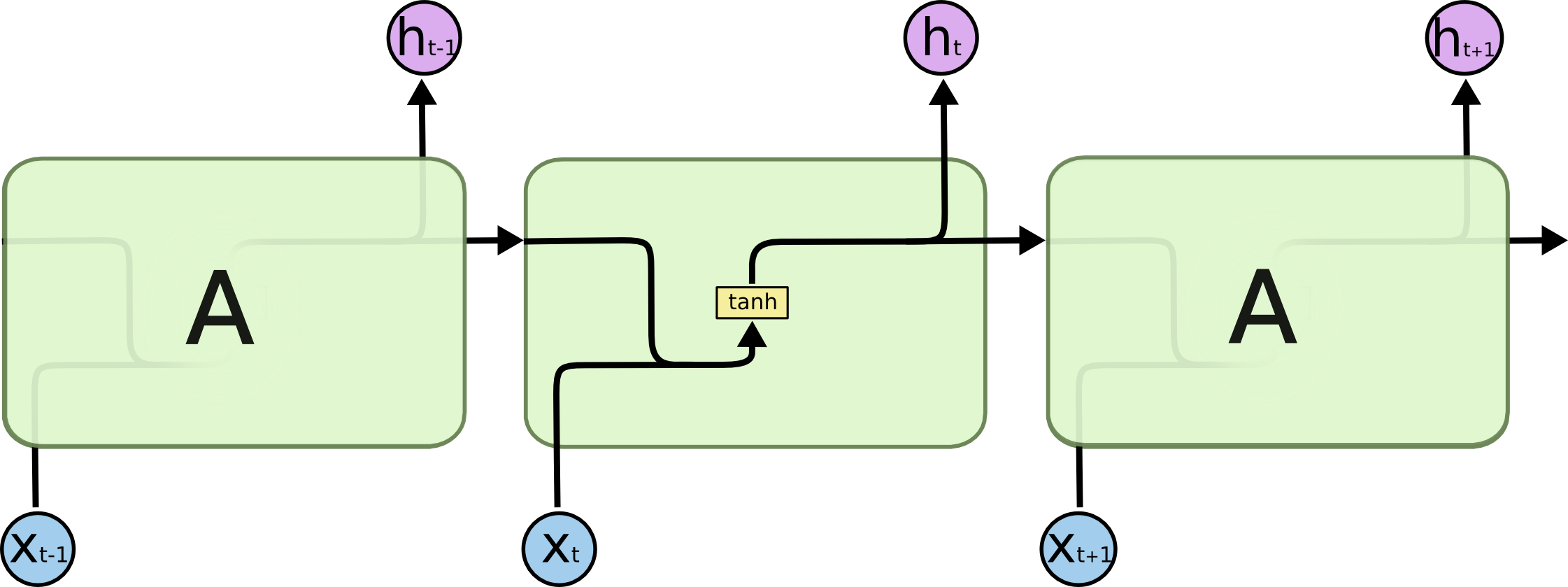

在TensorFlow中，BasicRNNCellm每一步输出的state和output相同，源代码如下:

def call(self, inputs, state):
  """Most basic RNN: output = new_state = act(W * input + U * state + B)."""

  gate_inputs = math_ops.matmul(
      array_ops.concat([inputs, state], 1), self._kernel)
  gate_inputs = nn_ops.bias_add(gate_inputs, self._bias)
  output = self._activation(gate_inputs)
  return output, output

公式如下:

$h_t=tanh(W_k[x_t,h_{t-1}]+b)$

或

$h_t=tanh(Wx_t+Uh_{t-1}+b)$

但是我个人认为应该是:

$h_t=tanh([x_t,h_{t-1}]*W+b) \tag{1}$

我也不知道为啥会都写作上面那两种形式.
eg:

import tensorflow as tf
import numpy as np

batch_size = 3
input_dim = 2
output_dim = 4

inputs = tf.placeholder(dtype=tf.float32, shape=(batch_size, input_dim))
cell = tf.contrib.rnn.BasicRNNCell(num_units=output_dim)
previous_state = cell.zero_state(batch_size, dtype=tf.float32)
output, state = cell(inputs, previous_state)
kernel = cell.variables
X = np.ones(shape=(batch_size, input_dim))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    output, state, kernel = sess.run([output, state,kernel], feed_dict={inputs: X})
    print(X.shape)
    print(kernel[0].shape)
    print(kernel[1].shape)
    print(previous_state.shape)
    print(state.shape)
    print(output.shape)
结果为:
(3, 2)
(6, 4)
(4,)
(3, 4)
(3, 4)
(3, 4)

分析: (kernel中是所有参数的list，此处是W和bias)根据公式(1),$output=([X,previous_state] * W+bias),即([(3, 2);(3, 4)]*(6, 4)+(4,)) = (3,4)$，代码中也较容易看出.
普通RNN梯度消失和梯度爆炸问题原因:

这是一个普通RNN图,其中$W_1$、$W_2$、$W_3$是不同时间步骤下的参数,我们要训练的就是这个参数,输出表达式为:
$f(w_1)=f_3(w_3f_2(w_2f_1(w_1)))$
求$W_1$的梯度:
$\frac{\partial f}{\partial W_1}=\frac{\partial f}{\partial f_3} \times W_3 \times \frac{\partial f_3}{\partial f_2} \times W_2 \times \frac{\partial f_2}{\partial f_1}$
这个讲解的相当清楚
若使用sigmoid函数,则每一次偏导都是一个(0,1)的数

初始化W全都(0,1),那么上诉公式中每一个因式都是(0,1),因此连乘的多了就会梯度消失

初始化W很大,大到乘以sigmoid函数后还是大于1,那么连乘的多了就会梯度爆炸

2.BasicLSTMCell
基本结构如图: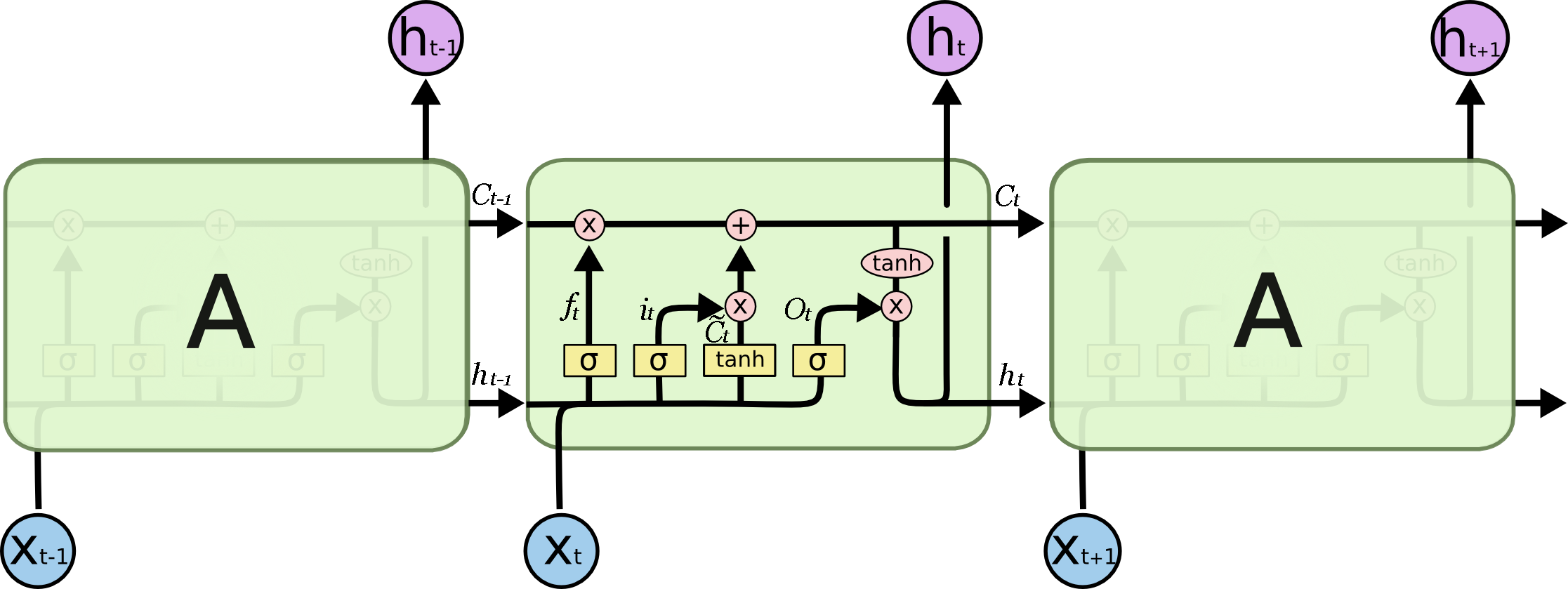

源码如下:

def call(self, inputs, state):
   """Long short-term memory cell (LSTM).
   Args:
     inputs: `2-D` tensor with shape `[batch_size, input_size]`.
     state: An `LSTMStateTuple` of state tensors, each shaped
       `[batch_size, self.state_size]`, if `state_is_tuple` has been set to
       `True`.  Otherwise, a `Tensor` shaped
       `[batch_size, 2 * self.state_size]`.
   Returns:
     A pair containing the new hidden state, and the new state (either a
       `LSTMStateTuple` or a concatenated state, depending on
       `state_is_tuple`).
   """
   sigmoid = math_ops.sigmoid
   one = constant_op.constant(1, dtype=dtypes.int32)
   # Parameters of gates are concatenated into one multiply for efficiency.
   if self._state_is_tuple:
     c, h = state
   else:
     c, h = array_ops.split(value=state, num_or_size_splits=2, axis=one)

   gate_inputs = math_ops.matmul(
       array_ops.concat([inputs, h], 1), self._kernel)
   gate_inputs = nn_ops.bias_add(gate_inputs, self._bias)

   # i = input_gate, j = new_input, f = forget_gate, o = output_gate
   i, j, f, o = array_ops.split(
       value=gate_inputs, num_or_size_splits=4, axis=one)

   forget_bias_tensor = constant_op.constant(self._forget_bias, dtype=f.dtype)
   # Note that using `add` and `multiply` instead of `+` and `*` gives a
   # performance improvement. So using those at the cost of readability.
   add = math_ops.add
   multiply = math_ops.multiply
   new_c = add(multiply(c, sigmoid(add(f, forget_bias_tensor))),
               multiply(sigmoid(i), self._activation(j)))
   new_h = multiply(self._activation(new_c), sigmoid(o))

   if self._state_is_tuple:
     new_state = LSTMStateTuple(new_c, new_h)
   else:
     new_state = array_ops.concat([new_c, new_h], 1)
   return new_h, new_state

公式如下:

$\begin{gather} f_t = \sigma(W_f[h_{t-1},x_t]+b_f) \\ i_t = \sigma(W_i[h_{t-1,x_t}]+b_i) \\ \widetilde C_t = \tanh(W_C[h_{t-1,x_t}]+b_C) \\ O_t = \sigma(W_o[h_{t-1},x_t]+b_o)\\ C_t = f_t*C_{t-1}+i_t*\widetilde C_t \\ h_t = O_t * \tanh(C_t) \end{gather}$

同理，我感觉应该是:

$\begin{gather} f_t = \sigma([h_{t-1},x_t]*W_f+b_f)\\ i_t = \sigma([h_{t-1,x_t}]*W_i+b_i) \\ \widetilde C_t = \tanh([h_{t-1,x_t}]*W_C+b_C) \\ O_t = \sigma([h_{t-1},x_t]*W_o+b_o)\\ C_t = f_t*C_{t-1}+i_t*\widetilde C_t \\ h_t = O_t * \tanh(C_t) \end{gather}$

eg:

import tensorflow as tf
import numpy as np

batch_size = 3
input_dim = 2
output_dim = 4

inputs = tf.placeholder(dtype=tf.float32, shape=(batch_size, input_dim))

cell = tf.contrib.rnn.BasicLSTMCell(num_units=output_dim)
previous_state = cell.zero_state(batch_size, dtype=tf.float32)
output, state = cell(inputs, previous_state)
kernel = cell.variables
X = np.ones(shape=(batch_size, input_dim))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    output, state,kernel = sess.run([output, state, kernel], feed_dict={inputs: X})
    print(X.shape)
    print(previous_state[0].shape)
    print(previous_state[1].shape)
    print(kernel[0].shape)
    print(kernel[1].shape)
    print(state[0].shape)
    print(state[1].shape)
    print(output.shape)
结果:
(3, 2)
(3, 4)
(3, 4)
(6, 16)
(16,)
(3, 4)
(3, 4)
(3, 4)

分析: (kernel是所有参数，即W和bias)根据上诉公式，在源码中求遗忘门:$f_t$,输入门$i_t$和$\widetilde C_t$s输出门$O_t$的代码为:
i, j, f, o = array_ops.split(value=gate_inputs, num_or_size_splits=4, axis=one)

这里也解释了为什么eg中kernel[0]是(6,16),因为代码中是将4个W同时初始化在一起，即（6,16）中其实是有4个W，并在上诉代码中分别计算，kernal[1]同理。这样得到的i,j,f,o应该都是(3,4),在源码中可以看出计算i,j,f,o是矩阵相乘，但是计算$C_t$和$h_t$是各个元素相乘,因此得到的$C_t$和$h_t$都是(3,4).

3.GRU

源代码为:

def call(self, inputs, state):
  """Gated recurrent unit (GRU) with nunits cells."""

  gate_inputs = math_ops.matmul(
      array_ops.concat([inputs, state], 1), self._gate_kernel)
  gate_inputs = nn_ops.bias_add(gate_inputs, self._gate_bias)

  value = math_ops.sigmoid(gate_inputs)
  r, u = array_ops.split(value=value, num_or_size_splits=2, axis=1)

  r_state = r * state

  candidate = math_ops.matmul(
      array_ops.concat([inputs, r_state], 1), self._candidate_kernel)
  candidate = nn_ops.bias_add(candidate, self._candidate_bias)

  c = self._activation(candidate)
  new_h = u * state + (1 - u) * c
  return new_h, new_h

eg:

import tensorflow as tf
import numpy as np

batch_size = 3
input_dim = 2
output_dim = 4

inputs = tf.placeholder(dtype=tf.float32, shape=(batch_size, input_dim))

cell = tf.contrib.rnn.GRUCell(num_units=output_dim)
previous_state = cell.zero_state(batch_size, dtype=tf.float32)
output, state = cell(inputs, previous_state)
kernel = cell.variables
X = np.ones(shape=(batch_size, input_dim))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    output, state, kernel = sess.run([output, state, kernel], feed_dict={inputs: X})
    print(X.shape)
    print(previous_state.shape)
    print(kernel[0].shape)
    print(kernel[1].shape)
    print(kernel[2].shape)
    print(kernel[3].shape)
    print(state.shape)
    print(output.shape)
结果:
(3, 2)
(3, 4)
(6, 8)
(8,)
(6, 4)
(4,)
(3, 4)
(3, 4)

Tensorflow中Rnn的实现

谢谢~~