softmax

参考原文

softmax优势

1. 计算loss公式方便
2. 反向传播容易计算

计算说明

$$z_4 = w_{41}*o_1+w_{42}*o_2+w_{43}*o_3 \\ z_5 = w_{51}*o_1+w_{52}*o_2+w_{53}*o_3 \\ z_6 = w_{61}*o_1+w_{62}*o_2+w_{63}*o_3$$

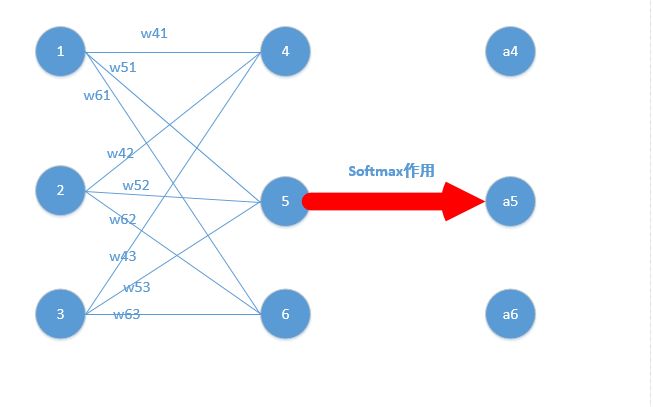
$z_4,z_5,z_6$分别代表结点4,5,6的输出
计算softmax

$$a_4=\frac{e^{z_4}}{e^{z_4}+e^{z_5}+e^{z_6}} \\ a_5=\frac{e^{z_5}}{e^{z_4}+e^{z_5}+e^{z_6}} \\ a_6=\frac{e^{z_6}}{e^{z_4}+e^{z_5}+e^{z_6}}$$

要求梯度,首先需要定义loss,计算交叉熵损失函数为:

$$Loss= -\sum_i y_i\ln a_i$$

其中,$y_i$是上诉$z_4,z_5,z_6$,$a_i$是标签。
看起来很复杂,其实实际情况下的$a_i$一般只是一个为1,其他都为0,故:

$$Loss = y_j \ln a_j$$

当标签为1的时候:

$$Loss = \ln a_j$$

也就是第一条优势:损失函数简单
下面我们计算梯度,如我要求出$w_{41},w_{42},w_{43}$的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可.

情况一:j=i,比如此时求$w_{41}$的偏导($a_4$对应的标签为1),则:

$$\frac{\partial Loss}{\partial w_{41}}=\frac{\partial Loss}{\partial a_4} \times \frac{\partial a_4}{\partial z_4} \times \frac{\partial z_4}{\partial w_{41}}$$

易知:

$$\frac{\partial Loss}{\partial a_4}=-\frac{1}{a_4} \\ \frac{\partial z_4}{\partial w_{41}} =o_1$$

关键点在于求$\frac{\partial a_4}{\partial z_4}$

$$\begin{align} \frac{\partial a_4}{\partial z_4} &= \frac{e^{z_4}(e^{z_5}+e^{z_6})}{e^{z_4}+e^{z_5}+e^{z_6}} \\ &= a_4(1-a_4) \end{align}$$

如图所示:

相乘得到最终公式:

$$\begin{align} \frac{\partial Loss}{\partial w_{41}} &=-\frac{1}{a_4} \times a_4(1-a_4) \times o_1 \\ &=(a_4-1) \times o_1 \end{align}$$

即:

$$\frac{\partial Loss}{\partial z_4}=a_4-1$$

形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可。

情况二:j!=i,比如此时求$w_{51}$的偏导,$a_4$对应的标签为1,则:

$$\frac{\partial Loss}{\partial w_{51}}=\frac{\partial Loss}{\partial a_4} \times \frac{\partial a_4}{\partial z_5} \times \frac{\partial z_5}{\partial w_{51}}$$

关键点在于求$\frac{\partial a_4}{\partial z_5}$

$$\begin{align} \frac{\partial a_4}{\partial a_5} &=-\frac{e^{z_4}e^{z_5}}{(e^{z_4}+e^{z_5}+e^{z_6})^2} \\ &= -a_4a_5 \end{align}$$

如图所示: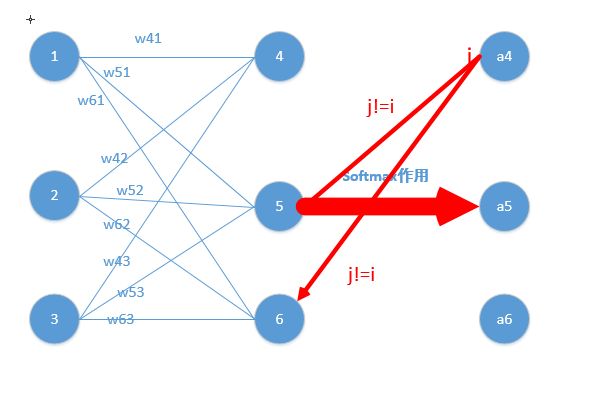

相乘得到最终公式:

$$\begin{align} \frac{\partial Loss}{\partial w_{51}} &=-\frac{1}{a_4} \times (-a_4a_5) \times o_1 \\ &=a_5 \times o_1 \end{align}$$

即:

$$\frac{\partial Loss}{\partial z_5}=a_5$$

形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可

举例说明

举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],
那么经过softmax函数作用后概率分别就是$[\frac{e^{2} }{e^{2}+e^{3}+e^{4}}
,\frac{e^{3} }{e^{2}+e^{3}+e^{4}} ,\frac{e^{4} }{e^{2}+e^{3}+e^{4}} ]$,[0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！！然后再根据这个进行back propagation就可以了