神经网络生成模型学习总结

生成模型

$\qquad$众所周知，神经网络是个判别模型，此处所指”生成模型”指的是功能性质，即利用神经网络生成我们需要的数据，比如对话生成/图像生成/语音生成。
$\qquad$试想，我们现在想生成一个图片，需要怎么做呢？

1. 需要知道我们要生成一个什么样图片,比如我们想生成一个卡通头像
2. 需要找到类似所需卡通图片的很多卡通图像
3. 用2中的所有图像训练一个模型
4. 给3中的模型一个输入，得到所需卡通头像

AutoRegression

AutoRegression

自回归是一种Step By Step的方式, 相关论文有:WaveNet、PixelRNN、PixelCNN
优点：对对话/语音这类顺序明显的类别比较友好
缺点：

1. 对图像而言，很难确定一个好的生成顺序
2. 在inference阶段，当前步骤严重依赖前一步骤
3. 慢

AutoEncoder

AutoEncoder

优点:

1. 无需Step By Step，可以并行生成
2. 生成数据更规则，一板一眼。

缺点：loss是对元素级别的监督度量，全局信息关注不足，因此模型泛化不够，两个非常接近的输入，可能输出天差地别。
举例说明：

你认为左图和右图中哪个更相似呢？很显然是B，但是它和输入图像差了5个pixel，而A只差了2个pixel，而按照AutoEncoder的方式训练，模型认为和A更相似。

Variational Autoencoder

$\qquad$现在想想，我们训练了这样一个模型，要怎么用呢？最简单的用法是把$Eocnder$编码后的向量(latent vertor)，保存下来，用的时候在用$Decoder$生成，但这仅仅是压缩的作用，显然大材小用了，我们其实想要的是,对于$Encoder$编码后的向量所符合的分布中，任意取一个向量都能产生合理的图片。 这样我们就能只保存$Decoder$和分布相关参数,从而产生出我们没见过的图片。很显然，现在的问题是，我们根本无法控制$Encoder$的输出分布，也就无法判断某一个向量是否符合该分布，这种情况下$VEA$出现了。
$\qquad$ VAE 其实最理想的控制$Encoder$分布的方式是模型训练好之后，用所有的训练输入通过$Encoder$各自得到一个向量，然后用这些向量得到分布，但是该方法几乎不可能，我们常用的方式类似最大似然，假设一个分布，然后用数据计算参数，VAE的思想是，对$Encoder$添加约束，强制使其输出符合高斯分布，那么模型训练好之后就能从该高斯分布中随机取向量生成没见过的图片了。
$\quad$说起来简单，但实际上VAE是一个实现起来简单，但是理解起来很复杂的模型，后续专门写一篇，这次就作为简单理解。

GAN

GAN

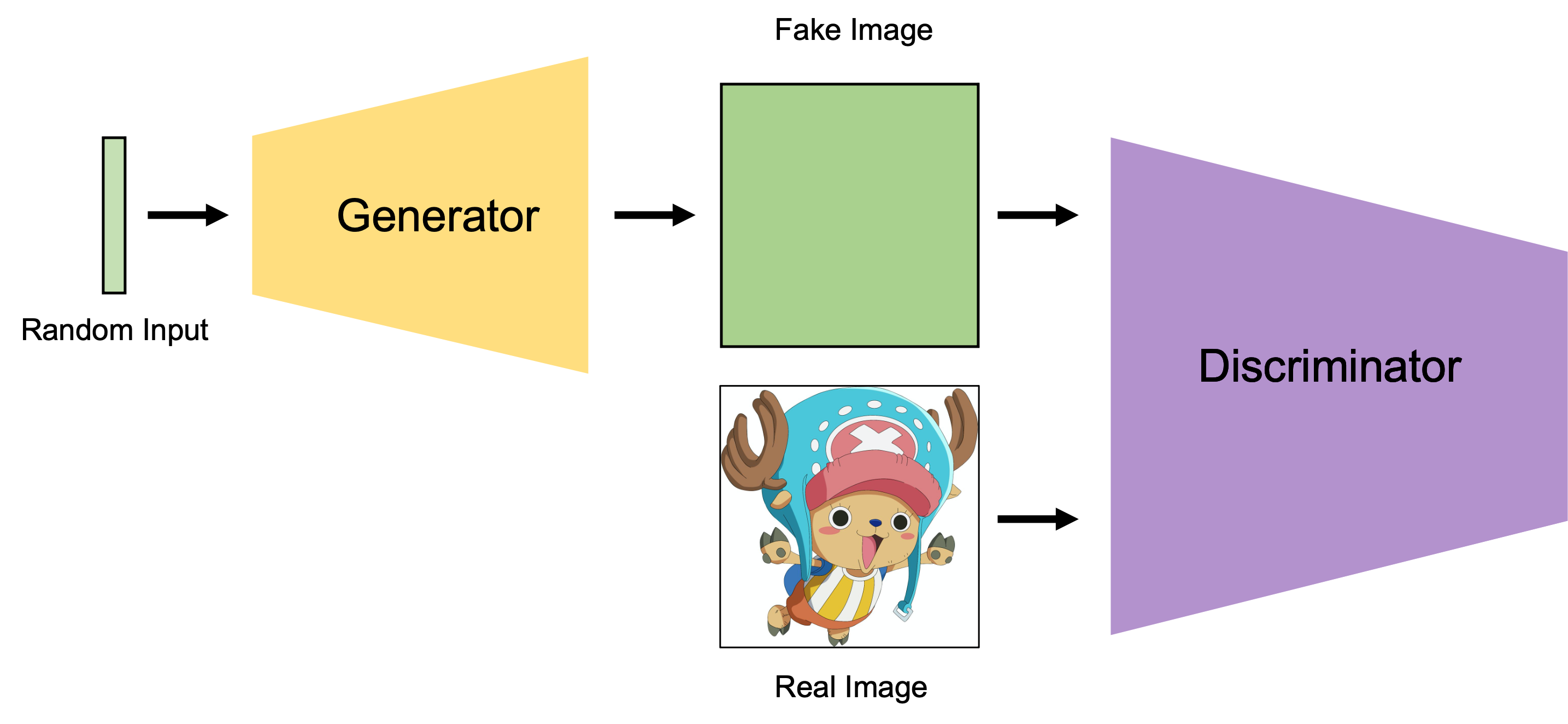
1. 从任意分布（如高斯分布）sample一个向量，输入Generator得到和所需图片相同size的输出
2. 把1中的输出当作副样本，从训练数据中sample一个正样本，以二分类的形式训练Discriminator(freeze Generator)。

3. 重新sample一个向量，输入Generator得到和所需图片相同size的输出，将其当作正样本输入Discriminator，计算loss 训练Generator(freeze Discriminator)
   上诉三个步骤是一个轮次。
   这里面有两个问题：

4. Generator可不可以自己学？
   理论是可以，但操作起来不行，如果这样做的话训练应该是这样一个流程：
   从任意分布（如高斯分布）sample一个向量，输入Generator希望得到和真实数据一样的分布，即$Generator$应该满足：

   $$G=arg\max_G\sum_i logp_g(x_i) \tag{1}$$

   这个很容易理解，其实就是一个最大似然估计而已，但是很显然，$G(x_i)$我们无从得知。因为我们在概率论中计算这种情况都是假设$G(x)$是某种分布再计算，但是神经网络非常复杂，根本不是假设某个分布就能做到的。

5. Discriminator可不可以自己学？
   可以，如果这样做的话训练应该是这样一个流程：
   首选sample一部分真实图片（正样本），随机初始化一些乱七八糟的图片（负样本），训练Descriminator，然后在求: $$x=arg\max_xD(x) \tag{2}$$ 令$x$为负样本在反复计算，知道收敛。 但问题是，公式（2）的计算也是很困难的。

GAN损失函数

论文中给出的损失函数是这样的：

$$\min_G\max_DV(D,G)=E_{x \sim p_{data}(x)}[logD(x)]+E_{z \sim p_z(z)}[log(1-D(G(z)))] \tag{3}$$

论文中说，这个损失函数相当于$JS(p_{data}(x)||p_g(x))$，现在我们来证明一下。

$$JS(p||q)=\frac{1}{2} KL(p||\frac{p+q}{2})+\frac{1}{2}KL(q||\frac{p+q}{2}) \tag{4}$$

首先需要意识到的是，$p_{data}(x)$、$p_g(x)$、$p_z(z)$是三个分布，指的是括号中变量的概率值，即可以看作一个函数。

$$\min_G\max_DV(D,G) = \int_x p_{data}(x)\times logD(x)+\int_zp_z(z)\times[log(1-D(G(z)))]dz \tag{5}$$

我们对(3)中的第二项进行积分换元：
假设$G(x)$是个可逆函数(该假设一般不成立)，则有：

$$z=G^{-1}(x) \qquad dz=G^{-1}(x)'dx \qquad p_g(x)=p_z(G^{-1}(x))G^{-1}(x)'dx \tag{6}$$

因此，带入公式(3)中可得:

$$\min_G\max_DV(D,G) = \int_x p_{data}(x)\times logD(x)+ p_g(x)\times[log(1-D(x))]dx \tag{7}$$

固定$G(x)$，让$D(x)$最大,令偏导为0:

$$\frac{\partial}{\partial D(x)}=\frac{p_{data}(x)}{D(x)}-\frac{p_g(x)}{1-D(x)}=0 \tag{8}$$

最终可得:

$$D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)} \tag{9}$$

因此，当$G(x)$固定时，$D^*_G(x) $最优解为公式(7)
而又有:

$$\begin{align} JS(p_{data}(x)||p_g(x))&=\frac{1}{2}\int_x p_{data}(x)log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}dx+\frac{1}{2}\int_x p_g(x)\log\frac{p_g(x)}{p_{data}(x)+p_g(x)}dx \\ &=log2+\frac{1}{2}\int_x p_{data}(x)\times logD^*_G(x)+ p_g(x)\times[log(1-D^*_G(x))]dx \\ &=log2+\frac{1}{2}\min_G\max_DV(D,G) \end{align} \tag{10}$$

这就得到了GAN损失函数和JS散度的关系。
实例代码地址

Flow

$\qquad$ 无论哪种生成模型，我们努力想要得到的无非两个东西，其一是$latent \quad vector$的分布，其二是$Generator$,这两者是成对的。基本原理就是如果从$latent \quad vector$输入$Generator$得到的结果分布$p_g$和真实数据分布$p_{data}$一致，那么我们就认为这个$latent \quad vector$的分布和$Generator$足够好.
$\qquad$ 在这个原理下就引入了两个难题，其一众所周知，数据分布是无法准确得知的，因此一般我们解决方式是强制固定分布来训练$Generator$，其二是如何衡量$Generator$的输出$p_g$和真实数据分布$p_{data}$足够近呢？两个分布距离一般用$KL$散度或$JS$散度，但不知道具体分布同样无法计算，$Gan$的方案是引入$Discriminator$，最后发现，诶，这个损失函数和$JS$散度等价，大功告成。
$\qquad$ 而Flow说，GAN算不了分布，我能算。
$\qquad$ 对于一个$Generator$而言，我们希望让其输出和真实数据分布越接近越好，即公式（1），但难点是$p_g(x_i)$未知，Flow的思想就是想方设法把这个分布用公式表达出来。
其基本原理是这样的，假设$z \sim \pi(z)$，经过$x=f(z)$函数的映射，得到$x\sim p(x)$,其中$f(z)$是可逆函数则有:

$$p(x)=\pi(z)\times |\det(J_f)| \tag{11}$$

详见此处，所以，我们可以把公式(1)改写为：

$$G=arg\max_G\sum_i log \pi(G^{-1}(x))\times|\det(J_{G^{-1}})| \tag{12}$$

那现在的问题是，我们无法保证一个普通的神经网络是可逆的，因此$G(x)$需要精心设计，而不能随便用。
首先需要确定的是，这里的雅可比矩阵必须是方阵(否则怎么算行列式？),因此$z$和$x$必须同形，flow的基本结构称为coupling layer，如图所示:

coupling layer 图中$F$和$H$可以是任意神经网络层。 $$ [x_1 \sim x_d] =[z_1 \sim z_d] \tag{13} $$ $$ [x_{d+1}\sim x_D]=F([x_1 \sim x_d]) \odot [x_{d+1} \sim x_D] \oplus H([x_1 \sim x_d]) \tag{14} $$ 根据这两条关系，我们很容易从计算$z$到$x$，即$G^{-1}(x)$ $$ G^{-1}(x)=concat[[x_1 \sim x_d],\frac{[x_{d+1}\sim x_D]-[b_{d+1}\sim b_D]}{[a_{d+1}\sim a_D]}] \tag{15} $$ 还需要计算$|\det(J_{G^{-1}})|$:

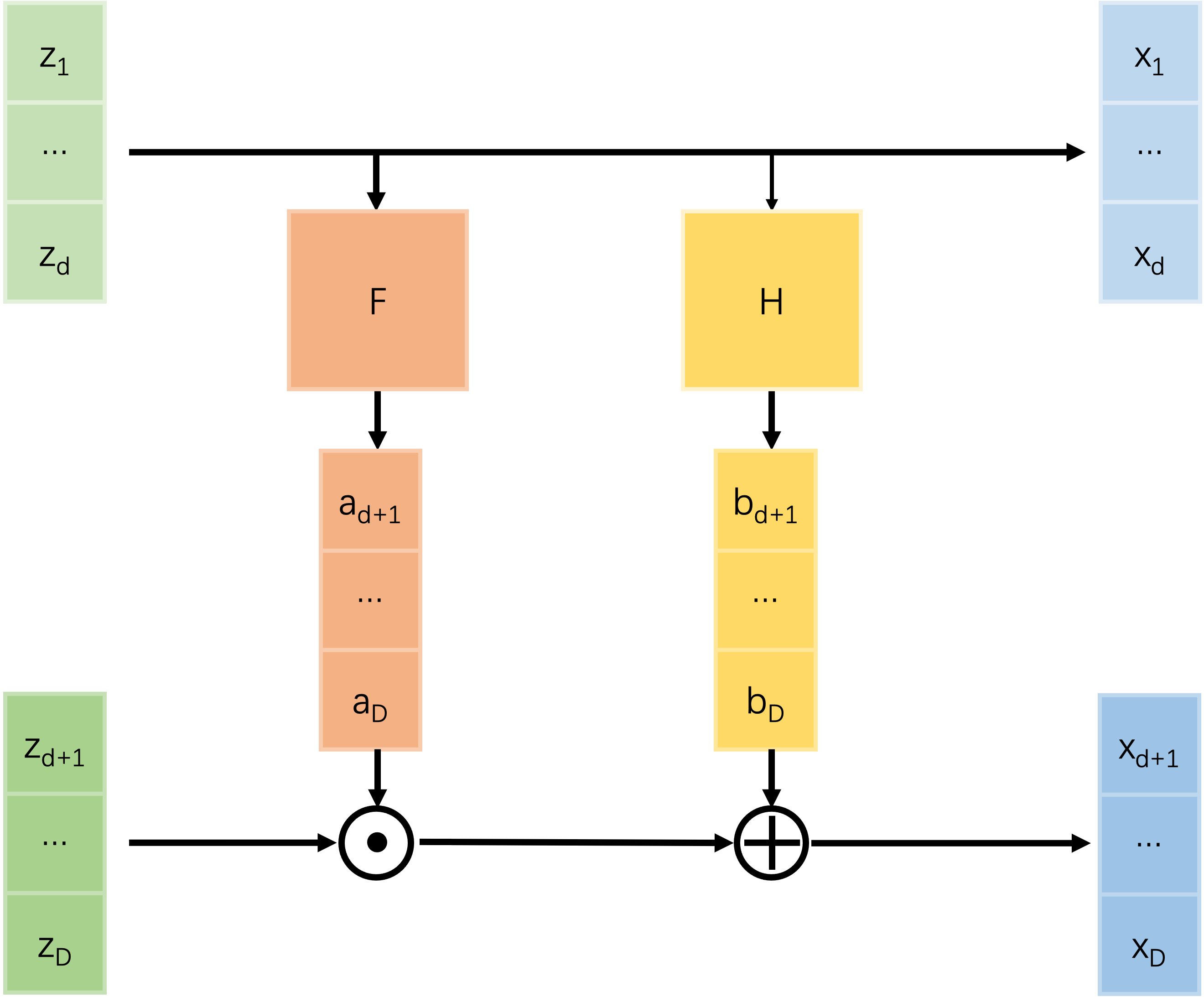
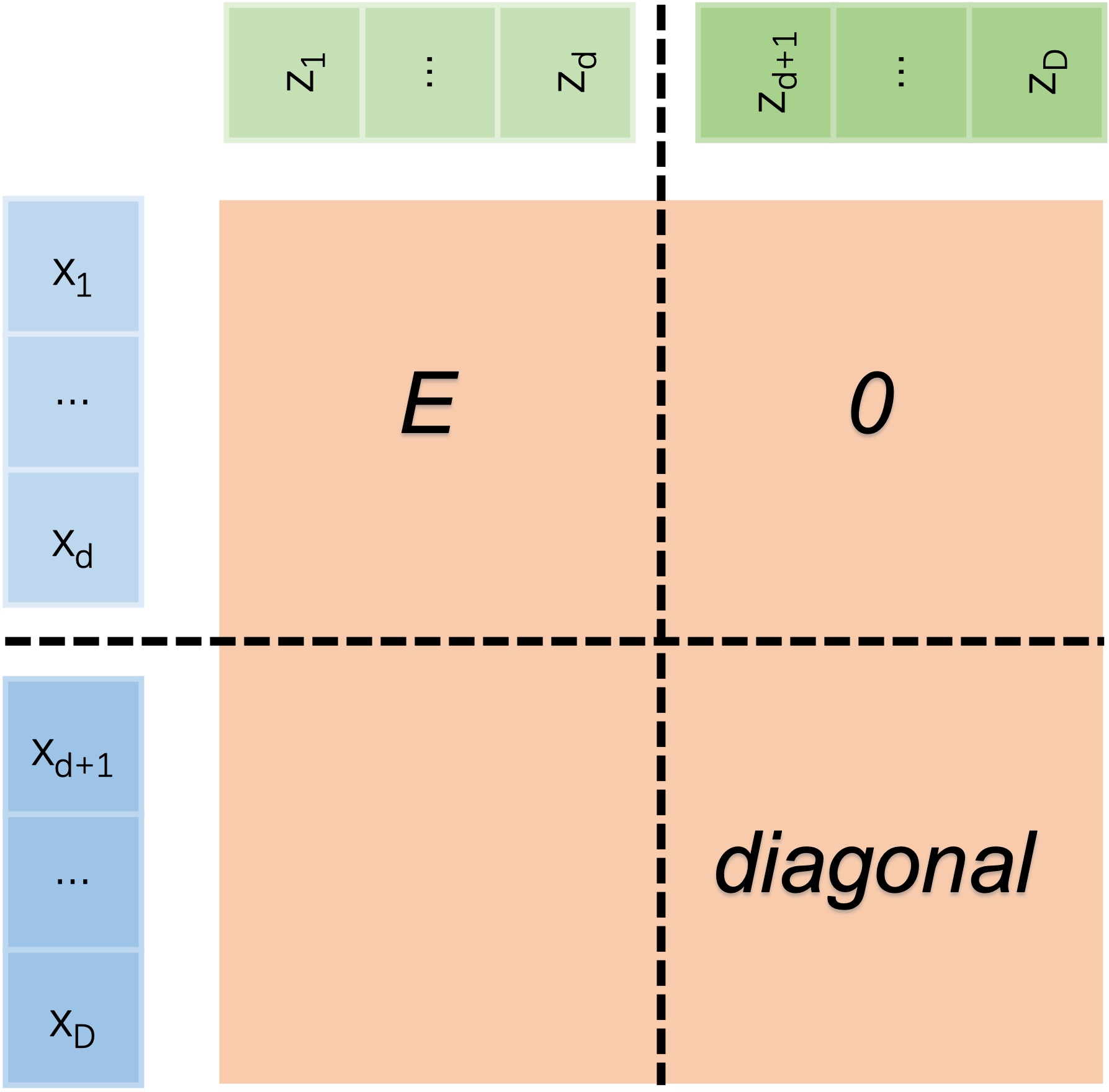
左上角是单位矩阵，右上角是0矩阵，左下角无关紧要，右下角是对角矩阵。

$$|\det(J_{G^{-1}})|=\frac{1}{|\det(dignoal)|}=\frac{1}{|\prod_{d+1}^Da_i|}\tag{16}$$

因此$G$即为所求。