学习算法的预测误差, 或者说泛化误差(generalization error)可以分解为三个部分: 偏差(bias), 方差(variance)和噪声(noise). 在估计学习算法性能的过程中,我们主要关注偏差与方差. 因为噪声属于不可约减的误差 (irreducible error).
符号说明
| 符号 | 含义 |
|---|---|
| x | 测试样本 |
| D | 数据集 |
| $y_D$ | x在D中的标记 |
| y | x的真实标记 |
| f | 训练集D上得到的模型 |
| f(x;D) | 训练集D上得到的模型在x下输出 |
| $\bar{f(x)}$ | 模型f对x的期望 |
1.y和$y_D$是有区别的,有些本来就标错了,即噪声。2.这是在不同的训练集D上得到的不同模型,下面的计算也是在不同训练集D下的均值。
误差定义
- 泛化误差:
均值
注意:方差和真实标记y无关,只和模型计算的实际值有关。
方差
噪声
偏差
对算法的期望泛化误差进行分解:
其中红色部分计算会得0:
1.
要谨记:其中带D得是变量,不带D的都是常量,也就是说$\bar{f(x)}$其实就是个数字,故有:
前两项得零,后两项等于:
也等于零
$E(XY)=E(X)E(Y)$的必要条件是X和Y相互独立,$E_D(f(x;D))E_D(y_D)$中$f(x;D)$和E_D(y_D)相互独立,因此可以分开。
2.
第二部分怎么得零的不太明白,难道是展开后$E_D(y)=E_D(y_D)$?
整理如图: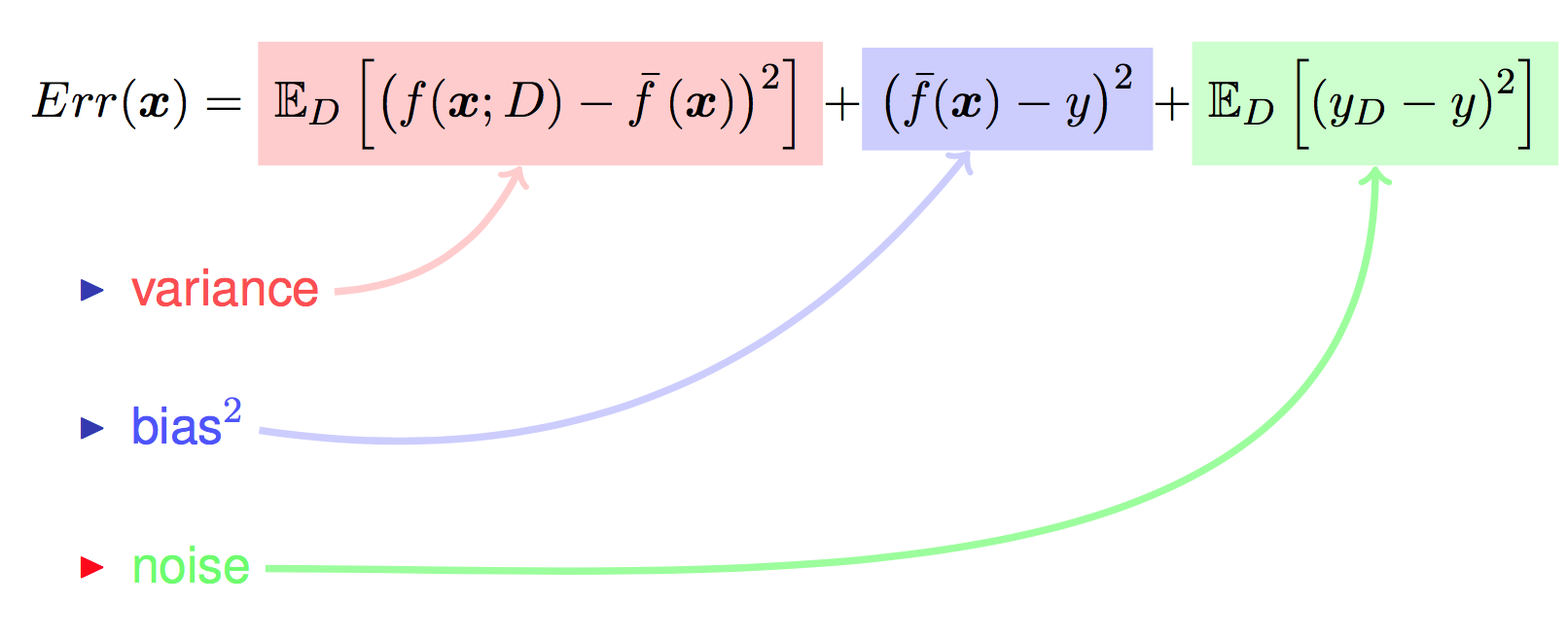
方差与偏差
以线性回归为例(训练集(train)、验证集(cv)、测试集(test)比例为6:2:2)
我们现在做的是在训练10个模型,次数依次从1到10,对于 多项式回归,当次数选取较低时,我们的 训练集误差 和 交叉验证集误差 都会很大;当次数选择刚好时,训练集误差 和 交叉验证集误差 都很小;当次数过大时会产生过拟合,虽然 训练集误差 很小,但 交叉验证集误差 会很大(关系图如下)。 图像如下:
Degree是次数
正则化参数$\lambda$
对于 正则化 参数,使用同样的分析方法,当参数比较小时容易产生过拟合现象,也就是高方差问题。而参数比较大时容易产生欠拟合现象,也就是高偏差问题.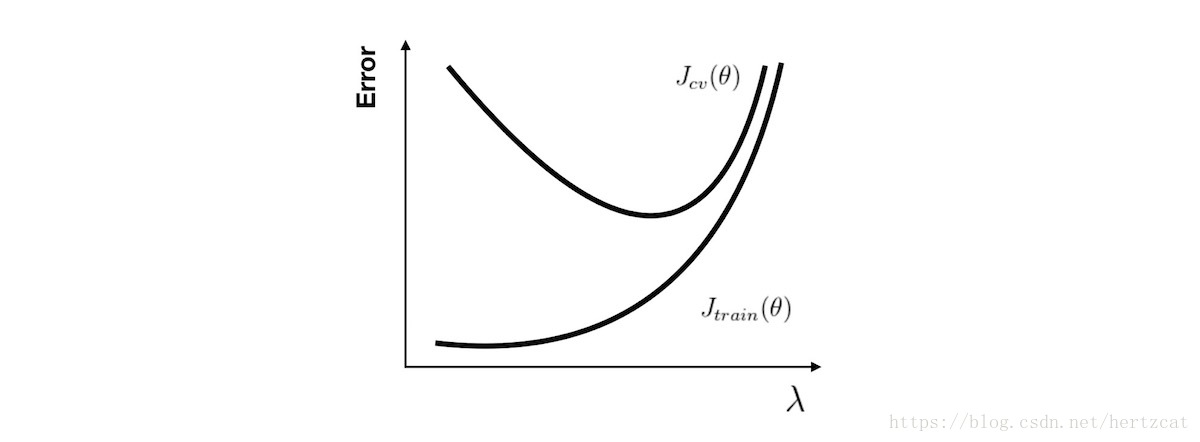
学习曲线
学习曲线 的横轴是样本数,纵轴为 训练集 和 交叉验证集 的 误差。所以在一开始,由于样本数很少,Jtrain(θ)Jtrain(θ) 几乎没有,而 Jcv(θ)Jcv(θ) 则非常大。随着样本数的增加,Jtrain(θ)Jtrain(θ) 不断增大,而 Jcv(θ)Jcv(θ) 因为训练数据增加而拟合得更好因此下降。所以 学习曲线 看上去如下图: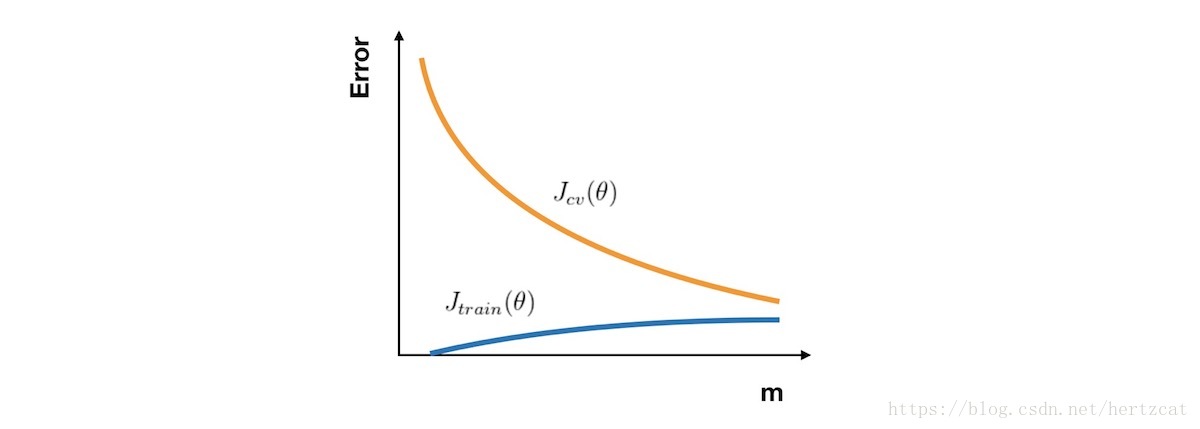
在高偏差的情形下,Jtrain(θ) 与 Jcv(θ) 已经十分接近,但是 误差 很大。这时候一味地增加样本数并不能给算法的性能带来提升。
在高方差的情形下,Jtrain(θ) 的 误差 较小,Jcv(θ) 比较大,这时搜集更多的样本很可能带来帮助。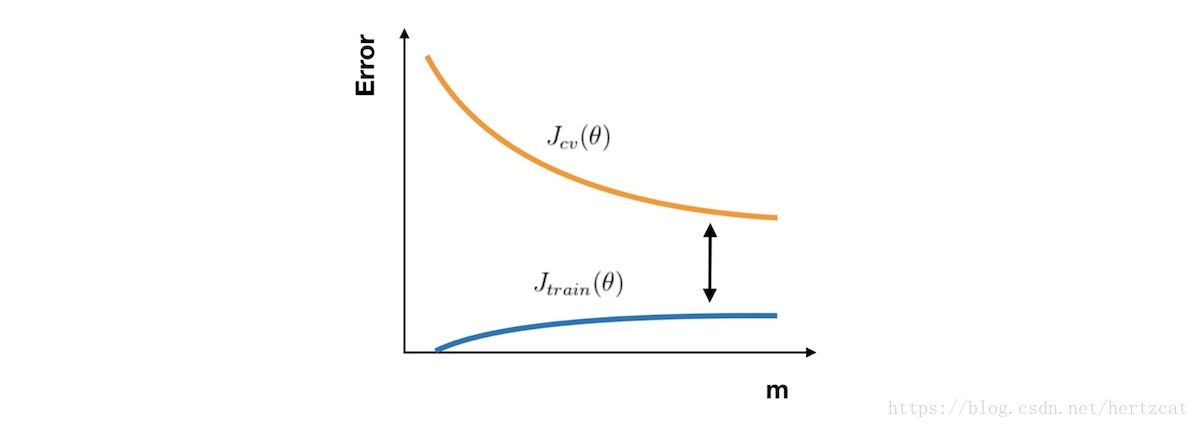
Bagging和Boosting
如何理解bagging是减少variance,而boosting是减少bias?
Bagging的意义是从总数据中每次随机取一部分,训练一个模型,这样做N次得到N个模型用投票的方式决定.(下面以N等于2为例)
这样得到的N个模型实际上是差不多的,Bagging的偏差表示为:$E(\frac{X_1+X_2}{2})=\frac{1}{N}E(X_2+X_2)=E(X_i)$,方差表示为$D(\frac{X_1+X_2}{2})$,如果$X$之间完全独立则等于$\frac{1}{4}D(X_1+X_2)=\frac{D(X_i)}{2}$,若$X$之间完全相同则等于$\frac{1}{4}D(X_1+X_2)=\frac{D(X_1)+D(X_2)+Cov(X_1,X_2)}{4}=\frac{4 \times D(X_i)}{4}=D{(X_i)}$
对于boosting而言每次都是为了降低$L(f(X),y)$,而降低损失函数就意味着降低偏差。由于各子模型之间是强相关的,于是子模型之和并不能显著降低variance(并未理解这句话。。。)
总结
- 获得更多的训练样本——解决高方差
- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差
- 尝试减少正则化程度λ——解决高偏差
- 尝试增加正则化程度λ——解决高方差
